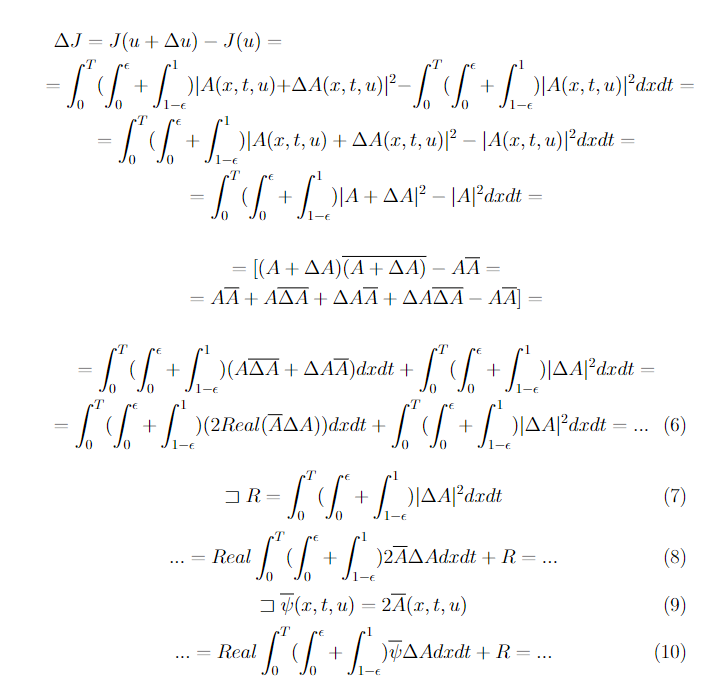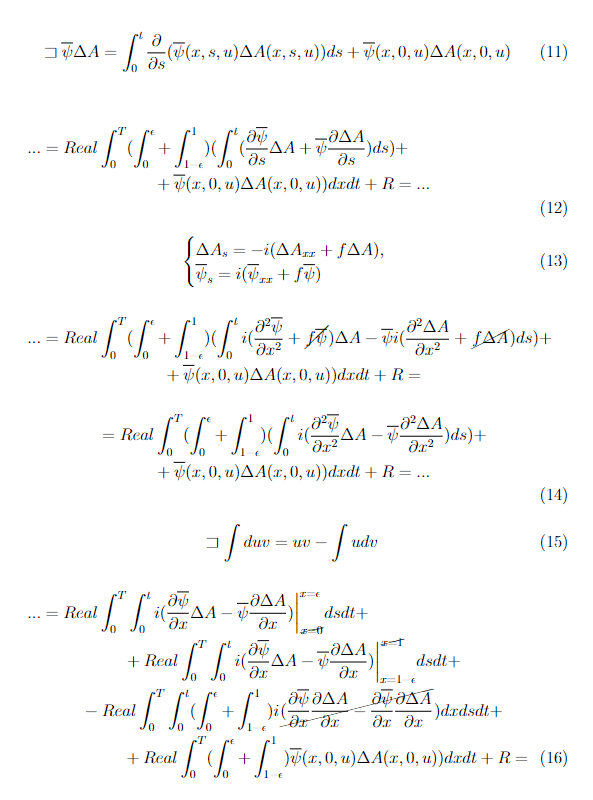Добрый день, есть краевая задача и функционал

И нужно найти

. Пытаюсь найти ее как линейную часть приращения.
Кажется, что я его нашел, за исключением нескольких очень непонятных моментов, ну и в целом прошу проверить, в основном сомневаюсь в 16-17 формуле - если бы интеграл был от 0 до 1 то сократилось бы всё, но у меня их два, тогда градиент должен получиться слишком сложным,
во что я искренне не верю и я не понимаю как дальше преобразовывать эти слагаемые в 17 формуле.
А может тут вообще всё неправильно ¯\_(ツ)_/¯
Скрины с латеха, постарался подробно расписать, надеюсь без опечаток: