Вопрос в том, можно ли ослабить требование дифференцируемости функции

на множестве

таким образом, чтобы утверждение теоремы осталось тем же? То есть можно ли в условии теоремы заменить фразу "дифференцируема на множестве

" на что-то из следующего списка:
1. дифференцируема на множестве

2. дифференцируема в точке

3. дифференцируема на каком-то другом подмножестве области определения

?
Ну, если Вам это очень-очень надо, то так и быть. Предполагаем дифференцируемость

в точке

. Открываем Зорича (том 1, стр.438):
Цитата:
... если

— дифференцируемая в точке

функция, то для любых векторов

и любых

функция имеет в точке

производную по вектору

и при этом


Ниже все производные берутся в точке

, а все векторы принадлежат пространству

(объяснение обозначения на стр.427), т.е. также относятся к точке

.
Введём ортонормированный базис

. Назовём вектор

градиентом функции

в точке

. Можно показать, что определение корректно, т.е. градиент не зависит от выбора ортонормированного базиса. Кроме того,

Нам надо показать, что

перпендикулярен множеству уровня

в

. Это значит, что

ортогонален любому вектору

,
касательному к множеству уровня. Проблема в том, что это понятие (или понятие
касательной гиперплоскости, как множества всех таких векторов) ещё не определено. В доказательстве из stackexchange касательная гиперплоскость определяется так:
Цитата:
The set of all vectors
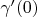
for all possible curves

forms the tangent hyperplane to

at

Мы же определим иначе: вектор

называется касательным к множеству уровня функции

в точке

, если

.
Тогда и

.