Исследовать на слабую сходимость и сходимость последовательность
![$x_n(t)=\sin^2nt\in L_2[0,1]$ $x_n(t)=\sin^2nt\in L_2[0,1]$](https://dxdy-04.korotkov.co.uk/f/f/9/d/f9de6fc4e8695a78d3e24aa1d7c3dba382.png)
Если бы было
![$[0,\pi]$ $[0,\pi]$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2385bc03c71e0b4fd8db3bac2e36c7f282.png)
, то была бы красивая интересная задача (ну по крайней мере для меня, который знает функан ограниченно).
Тогда

. Поскольку

(с единицей) полна на
![$[0,\pi]$ $[0,\pi]$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2385bc03c71e0b4fd8db3bac2e36c7f282.png)
(ну или не совсем поэтому, короче, это ортогональная система, при этом норма каждого из них ограничена), то она слабо сходится к нулю, а значит

слабо сходится к
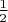
.
Сильной сходимости не будет, потому что расстояние между ортами

, при этом сдвиг его не меняет (тут по факту ненормированные, расстояние будет другое, но суть та же - не будет фундаментальности).
Но на
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
не совсем ясно... можно доказать, что, опять же, фундаментальности не будет.

, то есть при больших

расстояние будет конечно, например, больше

.
Но вот про слабую сходимость... я не думаю, что сходится слабо, сильно в этом сомневаюсь. Но как доказать не-сходимость?