Добрый день! Вспоминаю материал матана, решаю задачку по нахождению объема трехмерного тела, могли бы проверить мой ход решения, всё ли верно?
Задача: Найти объем тела, прямоугольные декартовы координаты точек которого удовлетворяют
неравенствам:
 Решение:
Решение:В трехмерном пространстве

- шар с центром в

,
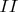
- цилиндр с центром проходящим также через

, наконец

- конус с вершиной в

. Я представил себе их визуально и решил разбить область на две:
1) область до пересечения конуса и цилиндра (их пересечение это

). Обозначим этот объем через

2) область выше, чем их пересечение, тут уже конус не будет играть никакой роли. Обозначим этот объем через


. Делаем цилиндрическую замену. Из неё я получаю, следующие пределы и интеграл:


. Делаем снова цилиндрическую замену, я получил следующий интеграл и пределы:

Суммируем и получаем ответ:
