Квазимногочлен

[Draeden]

$L(p) = a_0+a_1p+\ldots+a_p^n = (p-a)^mM(p)$
$M(a)\ne 0$
$f$ - многочлен

как показать существование многочлена $g$ ( $deg g \ne deg f$ ) такого, что

$L(p)(gt^me^{at})=fe^{at}$ ?

[RIP]

Я так понимаю, что $p$ — это оператор дифференцирования. Для $n\in\mathbb Z$, $\lambda\in\mathbb C$ определим линейное пространство над $\mathbb C$
$V_{n,\lambda}=\{P(x)e^{\lambda x}\mid P(x)\in\mathbb C[x],\deg P\leqslant n\}$
(считаем $\deg0=-\infty$).
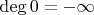
Легко проверить, что при $n\in\mathbb Z$, $\mu,\lambda\in\mathbb C$

$$(p-\mu)V_{n,\lambda}=\begin{cases}V_{n-1,\lambda},&\mu=\lambda,\\V_{n,\lambda},&\mu\ne\lambda\end{cases}$$

(для доказательства надо посмотреть, куда переходят $x^me^{\lambda x}$, и воспользоваться соображениями линейности). Отсюда уже легко следует требуемое (только $\deg g\leqslant\deg f$).
P. S. Надеюсь, не наврал.
P. P. S. Может, кто-нить ссылку кинет.

[Бодигрим]

RIP писал(а):

Я так понимаю, что $p$ — это оператор дифференцирования.

Упс. Вот теперь я таки присоединяюсь к звучавшим в предыдущих постах предложениях к Draeden писать несколько развернутее.

[ewert]

RIP писал(а):

(только $\deg g\leqslant\deg f$).

Всё же "равно" -- там отображение взаимно-однозначно. Иначе стандартный метод неопределённых коэффициентов был бы некорректным (т.е. соотв. система линейных уравнений для этих коэффициентов была бы некорректной). А это ведь не так.

[RIP]

Ну да, брякнул, не подумав. Но моё утверждение тоже верно.

[ewert]

формально -- безусловно