Нужны задачи на раскраску R^n, преимущественно R^2

[Zeddikus]

Нужны задачи на раскраску плоскости (или прямой или $\mathbb{R}^n, n\geqslant3$), у которых нет очевидного решения (в т.ч. и никем нерешённые). Для раскраски пространств желательно получить такие задачи, у которых нет аналога в плоскости, или если эта задача неочевидна, а аналог в плоскости очевиден.
Также можно привести пример задачи на раскраску $\mathbb{Z}^n$ или шестиугольной сетки, так как такие подзадачи могут возникать при опровержении гипотезы о той или иной раскраске всей плоскости.
Про хроматическое число плоскости знаю, этот пример не приводить.
Можно приводить примеры задач как с конечным числом цветов, так и со счётным или континуальным.

Примеры задач:
1. Можно ли покрасить плоскость в счётное множество цветов так, чтобы не нашлось ни одного одноцветного равностороннего треугольника (или правильного пятиугольника, прямоугольника единичной площади)?
2. Можно ли покрасить плоскость в счётное множество цветов так, чтобы не нашлось трёх точек $A,B,C$ таких, что все одного цвета и $AB=BC$?
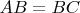
3. Можно ли так раскрасить шестиугольную сетку в 3 цвета, чтобы вершины любого равностороннего треугольника в этой сетке были окрашены ровно в 2 цвета? А если стороны треугольника проходят по сетке?
4. Можно ли покрасить плоскость в континуальное множество цветов (можно использовать не все цвета) так, чтобы вершины любого равностороннего треугольника были окрашены ровно в 2 цвета (для количества цветов 1 и 3 очевидно)?