Движение в центральном поле

[Mikhail Andropov]

Центральное поле $U(\vec{r})=\frac{kr^{2}}{2}$, где $k>0$, в ней находится частица, её масса $m$

Необходимо описать положение частицы в декартовой системе координат $x, y, z$, написав уравнения движения через Лагранжиан и решить их. А после - доказать, что траектория является эллипсом и найти период движения.

Я справился с уравнением Лагранжа и пришёл к следующим покоординатным уравнениям, например, для x: : $ \ddot{x}m +xk = 0$.

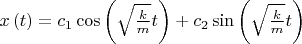
Решение этого дифференциального уравнения: $x\left(t\right)=c_{1}\cos\left(\sqrt{\frac{k}{m}}t\right)+c_{2}\sin\left(\sqrt{\frac{k}{m}}t\right)$. Через начальную скорость и координату по оси х можно выразить константы

Как мне быть с траекторией и периодом движения? Может быть, нужно сослаться на сохранение углового момента и как-то свести задачу к двумерной?

[Pphantom]

Тема перемещена из форума «Физика» в форум «Карантин»
по следующим причинам:

- отсутствуют собственные содержательные попытки решения задачи (в процессе решения настоятельно рекомендуется вспомнить, что движение не обязано являться одномерным).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.