У меня тут другая идея, после сравнения скорости кода Hugo с банальным кодом PARI, похоже код Hugo можно и ещё ускорить без всяких укорителей или добавления чего-то нового, всего лишь уменьшить одну из констант в коде. Вот и занялся проверкой и доказательством этой идеи.
Проверил, пока что досчитал до двухкратного ускорения перебора больших простых (которые дают или одно начальное число на проверку или не дают вообще) за счёт
гарантированного снижения верхнего предела докуда их нужно перебирать. Идея вот в чём. Чтобы уменьшить верхний порог для

при переборе в формуле
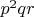
надо убедиться что начиная с некоторого достаточно большого

вообще нет решений для
любых возможных комбинаций

. В частности, код Hugo перебирает

начиная с пустых мест в паттерне, для которых можно принять

, т.е. перебирать

надо до

, что для

составляет 6.727e9 (что и видно в логах его программы, учитывая что

у него чуточку меньше). Если подставлять не в пустое место, то

и перебирать простые может понадобиться вплоть до

, что для

составляет почти 2e10. Но можно взять и
прямо проверить что для например

нет длинных решений для любых паттернов и любых

, ведь разных

не так уж и много, это не произвольное число, а всегда произведение двух различных простых, причём одно из них (я беру

, причём

) не меньше

(меньшие уже все размещены). Вот я и перебрал все такие

и все варианты

без привязки к паттернам вообще (потребовал лишь наличия числа
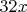
и правильных 5-ти чисел вокруг, это соблюдается для
любых цепочек длиной 10+), просто числа

(на чистом PARI, без дополнительных программ с недоказанной надёжностью), самое длинное что нашёл:
Код:
3*29*126506773^2:1392344834493997017: 20, 12, 8,192, 8, 12, 12, 12, 12, 12, 12, 12, 8, 48, 4, valids=8, maxlen=7
2*17*869483983^2:25704081487580505817: 4, 4, 8, 12, 12, 12, 12, 12, 12, 12, 8,192, 4, 32, 20, valids=7, maxlen=7
3*19*12201437869^2:8485879906050833886169: 16, 32, 32, 12, 12, 12, 12, 12, 12, 12, 4, 48, 8,128, 12, valids=8, maxlen=7
3*331*336983233^2:112762795427870362969: 8, 64, 32, 12, 12, 12, 12, 12, 12, 12, 16,192, 4, 4, 96, valids=7, maxlen=7
3*283*1292920201^2:1419224606584644460441: 4, 8, 4, 24, 64, 12, 12, 12, 12, 12, 12, 12, 8, 32, 48, valids=7, maxlen=7
И теперь в поиске решений по
любым паттернам длиной 11 можно перебирать

лишь до

(уже независимо от того в какое место паттерна подставляем

), что составляет почти ровно 3e9 (

так и выбиралось, для круглой цифры), более чем вдвое меньше используемой Hugo величины 6.727e9 (и почти в 7 раз меньше 2e10). И что самое прекрасное, этот порог действует не просто на
все паттерны, но и на
все переборы простых в них, не только на первый/верхний! А раз ускоряются все переборы больших простых, которые как раз страшно и тормозят пока что у Hugo, то и запускать переборы можно чаще и для чуть больших простых, что даст и дополнительный выигрыш в скорости.
Мне даст, предлагать реализовать это Hugo даже не буду (потому и пишу только на русском), он выше ясно высказался за универсальность в пику скорости, ну, это тоже правильный подход.