число инволюций всегда нечетно(и, следовательно, не равно нулю), а в группе нечетного порядка инволюции отсутствуют.
Второе легко доказывается через теорему Лагранжа.
А вот доказательство первого мне кажется очень громоздким и некрасивым.
Для доказательства первого буду использовать одну лемму: в любой конечной группе нечетное число элементов нечетного порядка.
Доказательство: Пусть в группе

элементы

имеют нечетный порядок. Каждый из этих элементов генерирует свою циклическую подгруппу в

. Будем считать, что

генерирует подгруппу

,

генерирует

и т.д. Т.к. генераторы всех этих циклических подгрупп имеют нечетный порядок, каждая из них содержит нечетное число элементов, а значит ни один из их элементов не имеет четный порядок(ведь в противном случае он сам будет образовывать циклическую подгруппу четного порядка внутри группы нечетного порядка, что невозможно по теореме Лагранжа). Т.к. каждая подгруппа cгенерирована каким-то элементом нечетного порядка и каждый элемент нечетного порядка генерирует какую-то подгруппу, объединение всех таких подгрупп будет содержать в себе все элементы нечетного порядка:

. При этом т.к. все объединяемые группы содержат только элементы нечетного порядка, их объединение будет содержать только элементы нечетного порядка:

. Следовательно,

, а значит

. Теперь попробуем определить четность правой части последнего равенства.
Понятно, что

. Первые два слагаемых нечетны. Вычитаемое: мощность подгруппы

. Это подгруппа группы нечетного порядка

, а значит по т. Лагранжа сама она тоже имеет нечетный порядок, а значит и ее мощность является нечетным числом, а значит правая часть последнего равенства - число нечетное.
Теперь найдем

. Первые два слагаемых нечетны. Вычитаемое: мощность множества

. Это множество является подгруппой

. Действительно, если

, то

и

, а значит и

, а значит

; если

, то

и

, а значит

, а значит

; следовательно, это действительно группа, причем все ее элементы принадлежат

, а значит это подгруппа в

, а т.к. порядок

- число нечетное, то и порядок этой группы тоже нечетен. Следовательно,

нечетно. Следовательно, учитывая все вышесказанное,

нечетно.
Аналогичным образом можно доказать, что

- число нечетное. А значит и

нечетно.
Теперь докажем основную теорему.
Раз в любой группе нечетное число элементов нечетного порядка, то, если
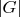
четно, то

(число элементов четного порядка из

) неизбежно должно быть нечетным. Каждый элемент четного порядка генерирует свою циклическую подгруппу в

, причем подгруппа эта будет четного порядка(т.к. генератор имеет четный порядок). Каждая такая циклическая подгруппа будет содержать инволюцию, причем ровно одну. Т.к. число элементов четного порядка нечетно, хотя бы одна инволюция всегда найдется.
Может так получится, что нескольким циклическим подгруппам будет соответствовать одна и та же инволюция.
Пусть инволюция

содержится в совокупности циклических подгрупп

Каждая из этих подгрупп сгенерирована элементом четного порядка

Следовательно и число элементов в каждой из них четно. При этом по доказанной выше лемме в каждой из них нечетное число элементов нечетного порядка, следовательно и число элементов четного порядка тоже нечетно. Один из них является обратным самому себе(инволюция

), остальные имеют обратный, отличный от них. Каждый из элементов четного порядка из любой такой циклической подгруппы образует свою собственную циклическую подгруппу четного порядка, причем она тоже содержит инволюцию

. Докажем последнее.
Пусть

циклическая подгруппа порядка, сгенерированная элементом

порядка

, а

- произвольный элемент четного порядка

. Понятно, что

, а значит

, что и требовалось доказать.
Получается, что все элементы четного порядка, содержащиеся в какой-то циклической подгруппе, содержащей инволюцию

образуют свои собственные циклические подгруппы, содержащие инволюцию

. Таким образом, все элементы четного порядка можно поделить на непересекающиеся классы, так, что элементам одного класса будет соответствовать одна и та же инволюция

. Докажем, что в каждом классе нечетное число элементов четного порядка.
Пусть инволюция

содержится в совокупности циклических подгрупп

Общее число элементов четного порядка в классе, соответствующем инволюции

можно посчитать, посчитав общее число элементов четного порядка во всех этих циклических подгруппах. В подгруппе

нечетное число элементов четного порядка. В подгруппе

тоже нечетное, при этом некоторые(минимум сама инволюция

) элементы из

нами уже учтены. Какое число новых элементов четного порядка мы обнаружим в

? Если какой-то элемент четного порядка содержится и в

и в

, то и обратный ему содержится в обеих циклических подгруппах, а значит вместе с любым элементом помимо инволюции

, содежащемся в обеих подгруппах, в обеих же подгруппах будет содеражатся и парный ему. Таким образом, у нас будет некоторые число пар элемент-обратный элемент и сама инволюция, т.е. общее число уже учтенных элементов будет нечетным, а значит, учитывая, что в

всего содержится нечетное число элементов четного порядка, новых элементов четного порядка в

мы обнаружим обязательно четное число.
Посмотрим далее на элементы четного порядка из

. Последовательно вычитая из их числа сначала число элементов, обнаруженных в

(обязательно число нечетное), а затем те элементы из

, которые не встречаются в

но встречаются в

(число четное, потому что для любого найдется обратный и инволюцию мы уже посчитали) мы получим число четное.
По аналогии каждая следующая циклическая подгруппа будет добавлять какое-то четное число элементов четного порядка, которые мы еще не учли. В итоге, посчитав все элементы четного порядка, мы получим сумму с одним нечетным и некоторым количеством четных слагаемых, а значит число нечетное. Следовательно, в каждом классе содержится нечетное число элементов четного порядка.
Если бы классов(а значит и инволюций) было четное число, общее число элементов четного порядка было бы числом, равным сумме четного числа нечетных чисел, а значит числом четным. Но мы знаем, что это не так. Следовательно, число инволюций нечетно.
Ну и заранее бесконечная благодарность вам, если вы сможете прочесть доказательство выше и найти в нем ошибку. Да и просто прочесть.