_hum_Пусть

- та самая величина.
1. Рассмотрим случайное блуждание на прямой, когда величина каждого шага - случайная, с плотностью

. Тогда

- (вроде бы) вероятность того, что после

шагов точка осталась на луче

. Может, что то из теории таких блужданий нам поможет?
2. (опять же, если я не ошибся при замене переменной) Имеем:

,
где

.
Рассмотрим еще интегралы

,
где

. Эти интегралы стандартной заменой сводятся к функции Лапласа (или:

есть вероятность того, что сумма

независимых, с плотностью

, больше 0; т.к., сумма нормальных - нормальна, то ответ выражается через

), и асимптотику

можно получить из известной асимптотики для нее. Осталось установить связь асимптотик для

и

. И тут будут только некие правдоподобные рассуденя.
Линии уровня

подынтегральной функции

-сферы с центром в точке

. В частности, сфера

для

касается плоскости

. Поэтому, для малых

кусок сферы

, попавший в

, похож на малый диск в

. Аналогично, для малых

кусочек сферы

, попавший в
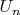
, похож на часть этого малого диска. Заметим, что (см. ниже) этот кусочек в

раз меньше куска (почти). Поэтому, в асимптотике

по сравнению с

появится дополнительный множитель

...Всё.
3. Пусть

- единичный шар в

, и

- гиперплоскость. Какую часть от "площади" диска

составляют точки, для которых

? Ответ:

Я это отношение сосчитал ручками для

и 4; получился красивый ответ. "Эта "ж"- неспроста", решил я. И правда, получилось.
Выложу эту задачку в Олимпиадном разделе.