Привет. Существует группа

c конечным числом образующих. Надо доказать, что число подгрупп

с заданным индексом

конечно.
Пусть

. Пусть

- всевозможные подмножества множества натуральных чисел мощности

, такие, что
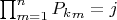
для любого

.
Тогда

- подгруппа

, причем индекс ее равен

.
С чего я так решил? Очевидно, что это подгруппа

. Чтобы индекс подгруппы был равен

сама подгруппа должна содержать

элементов. Мне кажется, что если построить подгруппу именно таким образом, то она будет иметь нужный порядок, но как это доказать я не знаю.
Вдобавок я не знаю, как доказать, что никаких других подгрупп

нужного порядка нет.