Пусть у нас есть некоторый прямоугольный проводящий контур, и в нём циркулирует ток

, а сам контур находится в однородном магнитном поле

, перпендикулярном плоскости контура, гравитации нет, контур покоится. Каково тогда будет распределение нормальной составляющей силы упругости стержня в одной из его сторон? С одной стороны, по уравнению моментов относительно оси, проходящей через точку

параллельно

получим:

где

- сила Ампера, действующая на участок
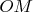
стержня длины

. То есть получим

. (

- нормальная компонента силы упругости на расстоянии

от точки

). С другой стороны по 2 з.Н. получим, что:

Но

по полученной ранее формуле, поэтому

. Почему такое противоречие возникает, и как от

зависит нормальная составляющая силы упругости? Кстати, если рассматривать бесконечно малый элемент стороны стержня, то там, вроде бы, тоже не всё сходится.
