У нас есть простая структура - предвзятая ладья двух типов. Здесь и далее открытый тур тождественен Гамильтонову пути.
Предвзятая ладья первого рода совершает открытые туры на специфической доске

, где

, а ячейки окрашены в белый или черный цвет в соответствии с двоичным представлением

. Ячейка окрашивается в белый цвет, если двоичная цифра равна

, и ячейка окрашивается в черный цвет, если двоичная цифра равна

. Предвзятая ладья на белой клетке движется только влево и в противном случае движется в любом направлении.
Предвзятая ладья второго рода совершает открытые туры на специфической доске

, где

, а ячейки окрашены в белый или черный цвет в соответствии с двоичным представлением

. Ячейка окрашивается в белый цвет, если двоичная цифра равна

, и ячейка окрашивается в черный цвет, если двоичная цифра равна

. Предвзятая ладья на белой клетке движется только влево и в противном случае движется только вправо.
Пусть

(
A284005) - число открытых туров предвзятой ладьей первого рода на соответствующей доске (двоичное представление

), оканчивающихся на любой клетке. Тогда имеет место быть рекурсия

где

(
A000120) - число единиц в двоичной записи

.
Как это можно доказать? Начнем с доски, заполненной лишь черными клетками, коих у нас будет

штук.

Исходную клетку мы выбираем

способами. По условию предвзятая ладья на черной клетке движется в любом направлении, соответственно следующую мы выбираем

, третью -

способами и т.д. По итогам имеем

открытых туров.
Добавим белую клетку где-нибудь посредине между черными:

Представим, что ее как и ранее нет, тогда мы вновь начинаем с

открытых туров. Теперь зададимся вопросом: сколькими способами мы можем вставить белую клетку в последовательность посещения черных? Пусть
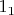
это черные клетки справа от белой, а

- черные клетки слева. Разберем на примере:

Очевидно, что перед
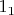
белая клетка стоять не может, поскольку предвзятая ладья на белой клетке движется только влево. Отметим возможные и невозможные положения через

и

:

Как мы видим на примере, белая клетка может стоять перед любой из

плюс в конце. Домножая на

имеем

открытых туров.
Добавим еще одну белую клетку справа от предыдущей и аналогично разберем на примере:

Ввиду того, что клетка расположена справа, перейти на нее с предыдущей белой мы не можем, что и отражено

после

. Зная, что исходная белая клетка может стоять лишь перед

, мы все также имеем

способов. Домножая, имеем

открытых туров. Аналогично для

имеем

открытых туров. Далее добавляем белые клетки справа:

Разберем на примере:

Здесь мы уже можем перемещаться как на

, так и на
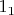
. После

белая клетка

стоять не может, итого имеем

способов. По аналогии в итоге будем иметь

.
Разбирая аналогичные примеры для

имеем

где

. Компактно выражение выше можно записать через

Вот код на pari для проверки:
Код:
default(parisizemax,10^9)
n=5
T(n,k)=if(n>0,if(k==0,valuation(n,2)+1,T(n\2,k-n%2)),0)
A003188(n)=bitxor(n, n>>1)
R(n,k)=T(A003188(n),k)
v=vector(2^n-1,i,vector(hammingweight(A003188(i)),j,R(i,j-1)))
for(i=1,2^n-1,print(v[i])) \\ просмотр массива ранов нулей и единиц в n
A069010(n)=(1 + (hammingweight(bitxor(n, n>>1)))) >> 1
a(n)=if(n==0,1,(sum(i=1,A069010(n),v[2*n][2*i]))!*prod(p=1,A069010(n),(1+sum(q=p,A069010(n),v[2*n][2*q]))^v[2*n][2*p-1]))
for(i=0,2^(n-1)-1,print(a(i)))
Имея теперь выражение для

, докажем рекурсию. Здесь надо вернуться к началу и еще раз подчеркнуть, что
Цитата:
Пусть

(
A284005) - число открытых туров предвзятой ладьей первого рода на соответствующей доске
(двоичное представление  )
), оканчивающихся на любой клетке.
Т.е. в конце у нас всегда будет как минимум один

.
Начнем с

. Добавляя

к последовательности нулей длиной

имеем
![$$a_1(2n)=\left(\sum\limits_{i=1}^{m}k_i\right)!\prod\limits_{p=1}^{m}\left(1+\sum\limits_{q=p}^{m}k_q\right)^{j_p+[p=1]}=\left(1+\sum\limits_{q=1}^{m}k_q\right)a_1(n)=(1+\operatorname{wt}(n))a_1(n)$$ $$a_1(2n)=\left(\sum\limits_{i=1}^{m}k_i\right)!\prod\limits_{p=1}^{m}\left(1+\sum\limits_{q=p}^{m}k_q\right)^{j_p+[p=1]}=\left(1+\sum\limits_{q=1}^{m}k_q\right)a_1(n)=(1+\operatorname{wt}(n))a_1(n)$$](https://dxdy-01.korotkov.co.uk/f/0/e/a/0ea00a9d8a9798c62a1bae535756744282.png)
Теперь разберем

. Возможны два случая:

и

В первом у нас
![$$a_1(2n+1)=(\sum\limits_{i=1}^{m}k_i+[i=1])!\prod\limits_{p=1}^{m}(1+\sum\limits_{q=p}^{m}k_q+[q=1])^{j_{p}}=(2+\sum\limits_{q=1}^{m}k_q)(1+\sum\limits_{i=1}^{m}k_i)!\prod\limits_{p=2}^{m}(1+\sum\limits_{q=p}^{m}k_q)^{j_p}$$ $$a_1(2n+1)=(\sum\limits_{i=1}^{m}k_i+[i=1])!\prod\limits_{p=1}^{m}(1+\sum\limits_{q=p}^{m}k_q+[q=1])^{j_{p}}=(2+\sum\limits_{q=1}^{m}k_q)(1+\sum\limits_{i=1}^{m}k_i)!\prod\limits_{p=2}^{m}(1+\sum\limits_{q=p}^{m}k_q)^{j_p}$$](https://dxdy-02.korotkov.co.uk/f/9/a/d/9ad51ffa6605ca3faa68a680ced952a182.png)

А во втором
![$$a_1(2n+1)=(1+\sum\limits_{i=1}^{m}k_i)!\prod\limits_{p=0}^{m}(1+\sum\limits_{q=p}^{m}k_q)^{j_{p}-[p=1]}=(1+\sum\limits_{q=0}^{m}k_q)(1+\sum\limits_{i=1}^{m}k_i)(\sum\limits_{i=1}^{m}k_i)!\prod\limits_{p=1}^{m}(1+\sum\limits_{q=p}^{m}k_q)^{j_p-[p=1]}$$ $$a_1(2n+1)=(1+\sum\limits_{i=1}^{m}k_i)!\prod\limits_{p=0}^{m}(1+\sum\limits_{q=p}^{m}k_q)^{j_{p}-[p=1]}=(1+\sum\limits_{q=0}^{m}k_q)(1+\sum\limits_{i=1}^{m}k_i)(\sum\limits_{i=1}^{m}k_i)!\prod\limits_{p=1}^{m}(1+\sum\limits_{q=p}^{m}k_q)^{j_p-[p=1]}$$](https://dxdy-03.korotkov.co.uk/f/e/d/2/ed240cda67a63f8e89a7eda02a653e9f82.png)

По совокупным итогам имеем


Что и требовалось доказать.
И еще одна маленькая деталь.
Пусть

(
A329369) - число открытых туров предвзятой ладьей второго рода на соответствующей доске (двоичное представление

), оканчивающихся на белой клетке. Тогда имеет место быть трансформация

Как это можно доказать? Рассмотрим на примере небольшой доски, скажем

. Заменим последовательно

единиц

нулями:
 - без изменений (
- без изменений ( единиц заменено
единиц заменено  нулями)
нулями) -
-  единица заменена
единица заменена  нулем
нулем - другой вариант предыдущего
- другой вариант предыдущего -
-  единицы заменено
единицы заменено  нулями
нулями
Результирующие значения

(ввиду того, что, опять-таки, мы работаем с двоичным представлением

) это и есть суммируемые

, такие, что

. В каждом из случаев мы суммировали пути, оканчивающиеся лишь на белых клетках, но т.к. черные были заменены на белые, мы по итогам имеем все возможные пути, оканчивающиеся на всех клетках.
Что и требовалось доказать.
Насколько строгими можно назвать доказательства? Требуют ли они уточнений? Могут ли они быть улучшены (например каким-нибудь образом упрощены)?