Не могу разобраться по учебнику ЛЛ-2, там как-то очень коротко и "на пальцах" выводится формула для компонент тензора энергии-импульса системы невзаимодействующих частиц.
Очень многие люди жалуются на то, что курс ЛЛ трудно читать, особенно в качестве первого учебника. Возможно, стоит поискать другой учебник.
Начинается вывод с того, что по аналогии с плотностью заряда, вводится формула для плотности массы.

Да. У нас есть инструмент — дельта-функция

, эта штука равна нулю при

, бесконечности при

, при этом интеграл по всему пространству

. Аналогичный интеграл по области

равен

, если точка

находится внутри

, равен

, если

снаружи

, а точно на границу

точечные массы у нас никогда попадать не будут.
Пусть внутри области

находится

частиц с массами
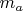
и радиус-векторами

, где

. Подберём такую подинтегральную функцию, чтобы объёмный интеграл от неё по

давал общую массу этих частиц:

Теперь подберём такую подинтегральную функцию, чтобы объёмный интеграл от неё давал общий импульс частиц. 3-импульс

-й частицы равен

(9.1).
С учётом (9.13),(9.14) компоненты

равны:

(греческие индексы пробегают значения

)
Значит, если взять плотность

, интеграл от неё даст полный импульс

частиц внутри

.
ЛЛ делают следующий шаг. Пусть

— некоторая гладкая векторная функция координат, определённая в

, причём в каждой точке

она совпадает с

. От номера частицы она уже не зависит. Она «имитирует» распределение 4-скоростей непрерывной среды. Для значения интеграла не важно, как

определена в точках, где нет частиц. И подинтегральную функцию можно с равным успехом записать в виде
 -- Вс ноя 07, 2021 19:54:00 --
-- Вс ноя 07, 2021 19:54:00 --Почему я рассматривал эти интегралы по объёму? Потому что плотность массы — это такая функция

, объёмный интеграл от которой по любой области

равен полной массе частиц (или непрерывного вещества) в этой области. Аналогично, плотность импульса — это такая функция, объёмный интеграл от которой по области

равен полному импульсу вещества, заключённого в этой области. Эти свойства «кандидатов в плотности» и проверялись.