Нашёл в одном известном
задачнике следующую задачку (253):
Сфера радиуса

заряжена зарядом

равномерно по поверхности и вращается вокруг одного из своих диаметров с угловой скоростью

. Найти магнитное поле внутри и вне сферы.
Ответ: при

напряжённость

, при

напряжённость

, где

.
В задачнике предлагается следующее решение (вкратце):
Плотность поверхностного тока

(полярная ось выбрана вдоль

).
Как следует из симметрии системы, векторный потенциал можно выбрать так, чтобы была отлична от нуля только компонента

, которая не будет зависеть от угла

. Поэтому

И дальше утверждается, что решение будет иметь вид

, где

можно найти из уравнения сверху и граничных условий.
Дальше я впал в ступор. Потому что искать можно двумя способами. Первый - представить уравнение в виде

, подставить

и сразу приравнять к

(уравнение Пуассона для векторного потенциала), как это делалось в предыдущих задачах. Так, очевидно, не получится, поскольку теперь

зависит ещё и от

.
Другой вариант - честно после подстановки посчитать лапласиан и снова приравнять его к

. Тогда

сократятся и получится уравнение

. Его решение

, которое тоже толком ничего не даёт: можно вычислить

. Перейдя к пределу

, получим
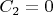
. А откуда брать

вообще не понятно, и если пытаться подобрать его исходя из ответа, получается ерунда вроде

.