Обобщённая задача вариационного исчисления

[PSP]

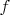
Как известно,задача вариационного исчисления состоит в том,чтобы найти функцию$f ,доставляющую минимум следующего функционала:
A[f] = \int_{x_1}^{x_2} L(x,f,f') dx..
Это приводит к уравнению Эйлера-Лагранжа:

$\frac{d}{dx} \frac{\partial L}{\partial f'} + \frac{\partial L}{\partial f}=0 $

которое и есть уравнение 2-го порядка.

Вопрос в том, известны ли задачи подобного рода на функционал:

A[f] = \int_{x_1}^{x_2} L(x,f,f', f'',f''') dx.?

И приводят ли они к уравнению ,подобному уравнениюЭйлера-Лагранжа,но 4-го порядка?

[Brukvalub]

Да, известны. Такие задачи иногда называют задачами вариационного исчисления со старшими производными, необходимое условие локального экстремума в такого рода задачах записывается в виде уравнения Эйлера-Пуассона. См., например, Алексеев В.М., Тихомиров В.М., Фомин С.В. — Оптимальное управление

[PSP]

Brukvalub писал(а):

Да, известны. Такие задачи иногда называют задачами вариационного исчисления со старшими производными, необходимое условие локального экстремума в такого рода задачах записывается в виде уравнения Эйлера-Пуассона. См., например, Алексеев В.М., Тихомиров В.М., Фомин С.В. — Оптимальное управление

Спасибо! Нашёл и скачал эту книгу.То, что надо!

Вечером или завтра опишу задачу, связанную с ней.

[PSP]

Brukvalub,ещё раз спасибо!
Задачу решил, после этой книги решение оказалось простым .
Но появился вопрос:

Уравнения Эйлера-Пуассона в задачах вариационного исчисления со старшими производными есть аналог уравнения Эйлера-Лагранжа в классике.
А как известно, уравненияю Эйлера-Лагранжа соответстуют уравнения Гамильтона.
Тогда какие же уравнения,похожие на уравнения Гамильтона, соответствуют уравнениям Эйлера-Пуассона?

[Не_вари_козла]

А что здесь будет аналогом энергии?

[PSP]

Не_вари_козла писал(а):

А что здесь будет аналогом энергии?

Чтобы найти ответ на этот вопрос,мне надо вспомнить конкретно, как линейное дифференциальное уравнение n-го порядка можно свести к системе линейных дифференциальных уравнениий 1-го порядка.
Вроде бы это делается с помощью контактных преобразований?
Кто помнит?
Или я что-то перепутал и так сделать нельзя?
(Кстати, тут речь о линейных дифференциальных уравненииях с постоянными коэффициентами пока)

[Brukvalub]

PSP писал(а):

Чтобы найти ответ на этот вопрос,мне надо вспомнить конкретно, как линейное дифференциальное уравнение n-го порядка можно свести к системе линейных дифференциальных уравнениий 1-го порядка.
Вроде бы это делается с помощью контактных преобразований?
Кто помнит?

Я бы просто нужное число раз обозначил новой переменной каждую из производных.

[zoo]

PSP писал(а):

Уравнения Эйлера-Пуассона в задачах вариационного исчисления со старшими производными есть аналог уравнения Эйлера-Лагранжа в классике.
А как известно, уравненияю Эйлера-Лагранжа соответстуют уравнения Гамильтона.
Тогда какие же уравнения,похожие на уравнения Гамильтона, соответствуют уравнениям Эйлера-Пуассона?

см Дубровин Новиков Фоменко Современная геометрия

[PSP]

zoo писал(а):

PSP писал(а):

Уравнения Эйлера-Пуассона в задачах вариационного исчисления со старшими производными есть аналог уравнения Эйлера-Лагранжа в классике.
А как известно, уравненияю Эйлера-Лагранжа соответстуют уравнения Гамильтона.
Тогда какие же уравнения,похожие на уравнения Гамильтона, соответствуют уравнениям Эйлера-Пуассона?

см Дубровин Новиков Фоменко Современная геометрия

Посмотрел.Там Эйлера-Пуассона вообше не рассматриваются..

[zoo]

PSP писал(а):

zoo писал(а):

PSP писал(а):

Уравнения Эйлера-Пуассона в задачах вариационного исчисления со старшими производными есть аналог уравнения Эйлера-Лагранжа в классике.
А как известно, уравненияю Эйлера-Лагранжа соответстуют уравнения Гамильтона.
Тогда какие же уравнения,похожие на уравнения Гамильтона, соответствуют уравнениям Эйлера-Пуассона?

см Дубровин Новиков Фоменко Современная геометрия

Посмотрел.Там Эйлера-Пуассона вообше не рассматриваются..

Ну еще посмотрите
Дубровин Новиков Фоменко Современная геометрия Наука 1979
прямой ответ на Ваш вопрос: стр 692 параграф"Вариационные задачи с высшими производными"

[PSP]

zoo писал(а):

PSP писал(а):

zoo писал(а):

PSP писал(а):

Уравнения Эйлера-Пуассона в задачах вариационного исчисления со старшими производными есть аналог уравнения Эйлера-Лагранжа в классике.
А как известно, уравненияю Эйлера-Лагранжа соответстуют уравнения Гамильтона.
Тогда какие же уравнения,похожие на уравнения Гамильтона, соответствуют уравнениям Эйлера-Пуассона?

см Дубровин Новиков Фоменко Современная геометрия

Посмотрел.Там Эйлера-Пуассона вообше не рассматриваются..

Ну еще посмотрите
Дубровин Новиков Фоменко Современная геометрия Наука 1979
прямой ответ на Ваш вопрос: стр 692 параграф"Вариационные задачи с высшими производными"

Да,действительно есть...!!!!К моему диву!!!Спасибо!!!Вот не думал там найти!!

[PSP]

А есть ли что-нибудь для темы "Вариационные задачи с высшими производными" нетчто вроде работ по теореме Нётер и законах сохранения?

Увы..нигде нету...