Арнольд, Математические методы классической механики, п. 49
Интегрируемые системы:
Цитата:
Предположим, что на симплектическом

-мерном многообразии даны

функций в инволюции

Рассмотрим множество уровня функций


Предположим, что на
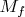

функций

независимы (т. е.

1-форм

линейно независимы в каждой точке
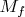
).
Тогда:
<...>
4) Канонические уравнения с функцией Гамильтона

интегрируются в квадратурах.
есть ли строгое определение "интегрируемости в квадратурах", подходящее к вышенаписанному, в частности, можно ли доказать, что какое-нибудь дифференциальное уравнение

с нерациональной

не интегрируется в квадратурах?
В "дифференциальной алгебре" доказывается "неинтегрируемость в квадратурах", например, уравнения Эйри

(Kaplansky, An introduction to differential algebra, § 26). Определение "интегрируемости в квадратурах" там есть, но оно, как я понимаю,
не такое, как то, что подразумевает Арнольд: в дифференциальной алгебре можно брать рациональные функции, первообразные, экспоненты и функции, неявно заданные
алгебраическими уравнениями

, где

-- присоединяемая функция, а

-- уже имеющиеся (точную формулировку смотрите у Капланского, теорема 6.6); а у Арнольда можно брать рациональные функции, первообразные и неявно заданные функции, только непонятно, какие именно:
Арнольд, М. м. кл. мех., § 50 ``Переменные действие -- угол'', конец писал(а):
Заметим теперь, что все наши построения содержат лишь «алгебраические» операции (обращение функций) и «квадратуру» — вычисление интеграла. Таким образом, задача интегрирования канонической системы

уравнений, у которых известны

первых интегралов в инволюции, решается в квадратурах, что и доказывает последнее утверждение теоремы.
(Имеется в виду обращение относительно композиции; при этом в доказательстве также используется взятие функции, заданной неявно уравнением

.)
Интегрирование в квадратурах означает предъявление алгоритма из конечного числа операций, позволяющего найти все решения уравнения. В число разрешенных операций включаются все алгебраические операции над функциями, простые квадратуры (вычисление интегралов от функций одного переменного), а также эффективное использование теоремы о неявных функциях.