Вопросы про сходимость в топ. пространстве

[yovska]

Утверждение:

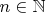
Для каждого $n \in \mathbb N$ положим $C_n = \{(n, 1), (n, 2), (n, 3), (n, 4),\ldots \}$ и положим $X = \cup_{n\ge1}C_n, X^+ = X \cup \{(0,0)\}.$ Дайте $X^+$ топологию, объявив $G \subseteq X^+$ открытым тогда и только тогда, когда: либо $(0,0) \not \in G$, либо $\exists n_0 \in \mathbb N$ такое, что $\forall n \ge n_0, \ C_n \setminus G$ конечно. Докажите, что никакая последовательность в $X$ не может сходиться к $(0,0)$.

Доказательство:

Предположим, если возможно, что существует последовательность $(z_i) \to (0, 0)$ в $X^+$, где $z_i = (x_i, y_i) \in X$. По обычным причинам каждая подпоследовательность $(z_i)$ также будет сходиться к $(0, 0)$.

Случай 1. Один отдельный «столбец» $C_n$ может включать $z_i$ для бесконечного количества $i$. Если так, то эти $z_i$ образуют подпоследовательность. И эта подпоследовательность не сходится к $(0, 0)$, потому что $\{(0, 0)\} \cup C_{n + 1} \cup C_{n + 2} \cup C_{n + 3} \cup \ldots$ - открытая окрестность $(0, 0)$, в которую подпоследовательность не входит. Противоречие!

Случай 2: в противном случае положим $N = X^+ \setminus (\text{область значений } (z_i))$, и это множество пропускает только конечное количество элементов в каждом столбце, поэтому это открытая окрестность $(0, 0)$, в которую последовательность не может войти. Противоречие.

Мои вопросы о приведенном выше доказательстве:

- Чем авторы руководствуются при разбиений док-ва на случаи или как они строят последовательности? Во втором случае мы берем конечное число элементов из каждого столбца для построения подпоследовательности, а в первом мы берем бесконечное количество элементов из каждого столбца для построения подпоследовательности, но рассматриваем только один. Это верно?

- Откуда мы знаем $\{(0,0)\} \cup C_{n + 1} \cup C_{n + 2} \cup C_{n + 3} \cup \ldots$ -- это открытая окрестность точки $(0,0)$? Мы знаем ${(0,0)} \not \in C_{n + i}$ для $i\ge 1$, поэтому $\cup_{i\ge1}C_{n + i}$ открыто. Но $(\cup_{i\ge1}C_{n + i}) \cup \{(0,0)\}$ тоже открытo? Как?

- Где в доказательстве мы используем определение топологии, данное в утверждении?