Используя разложение, рекомендованное realeugene, получены первые результаты спектрального анализа.
В "терминологии комплексных амплитуд" пространственное представление по

имеет вид:
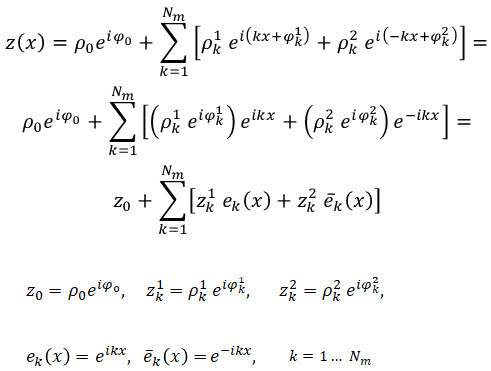
Подставив в это разложение точки,

, в которых проводилось измерение, получим

уравнений:
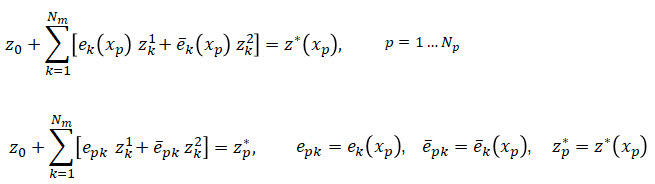
Записав уравнения относительно действительных и мнимых частей неизвестных:
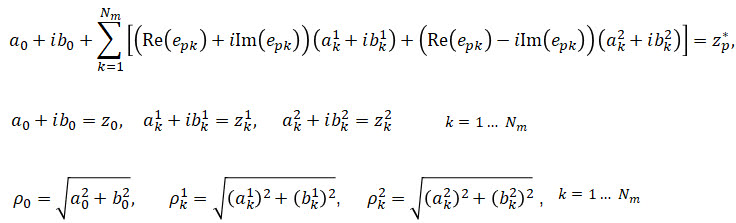
Окончательно получим систему 22-х линейных уравнений относительно неизвестных

:
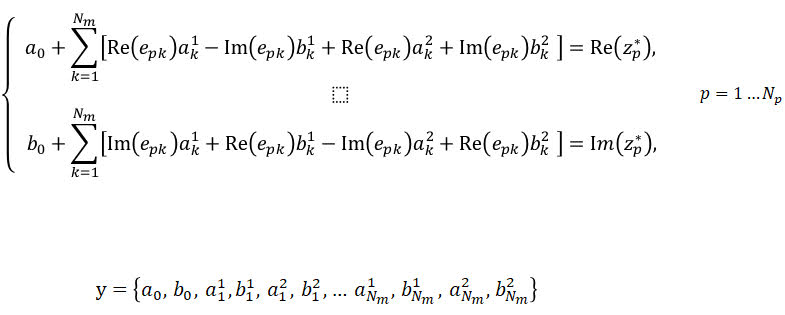
Здесь в правой части - результат преобразования Фурье по времени (при фиксированной частоте), то есть правая часть вычисляется и импортируется из Testlab.
Реализовав решение этой системы уравнений в Matlab (пока рассмотрена только нормальная составляющая ускорений) получились вот такие спектры.
40-я временная гармоника в Сечении 1 (середина статора):
Оси: частота в [Hz], Wave number, Amplitude в [g]. Датчики сертифицированы только до 10 kHz, поэтому частота отображается по 10500 Hz.
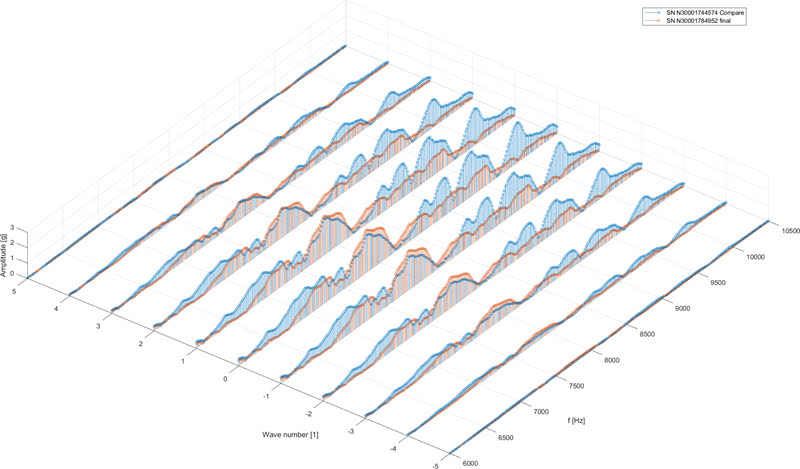
Оранжевый спектр соответствует малошумному мотору, который был отобран как "golden sample" по результатам тестирования вибрации непосредственно на сборочной линии, а синий спектр - соответствует шумному мотору, который рекламировали и прислали назад с просьбой установить причину шумности. Причина пока непонятна, но четко видно что амплитуды вибрации критических гармоник (40-й и 48-й) у рекламированного мотора заметно выше.
40-я временная гармоника в Сечении 2 (Non drive end):
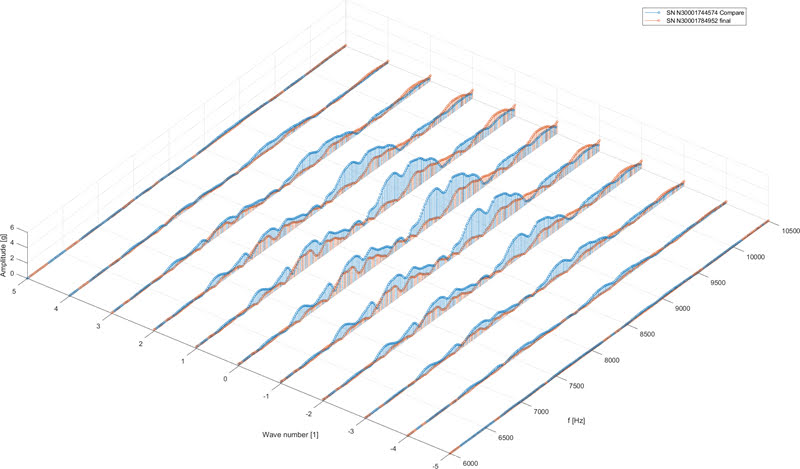
40-я временная гармоника в Сечении 3 (Drive end):
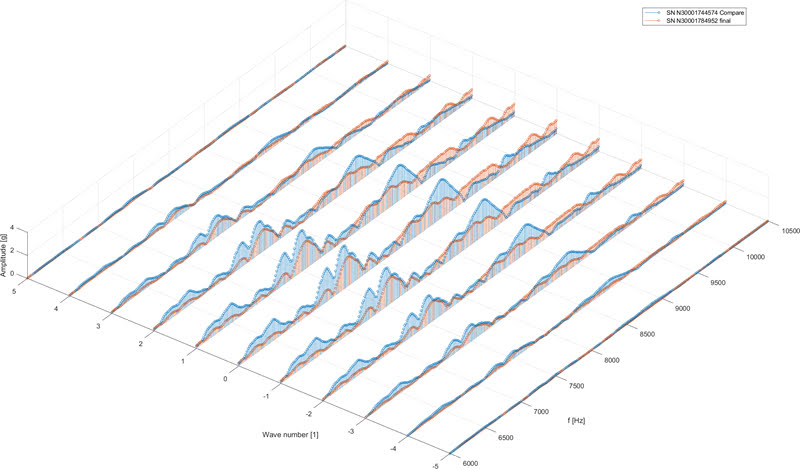
48-я временная гармоника в Сечении 1 (середина статора):
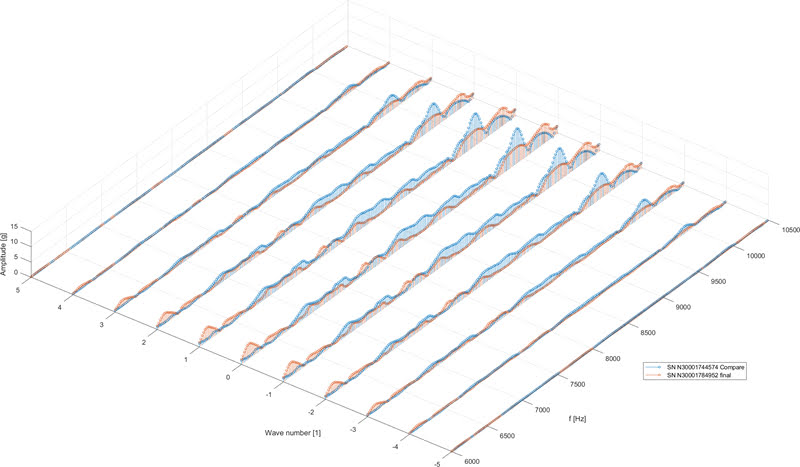
48-я временная гармоника в Сечении 2 (Non drive end):

48-я временная гармоника в Сечении 3 (Drive end):
