Здравствуйте! Прошу помочь разобраться в некоторых моментах в различных системах счисления, для примера, десятичной и семеричной.
Непонятно вот что: существует ли цифра для обозначения числа-основания для какой-либо системы счисления в самой этой системе счисления?
Поясню, что имею в виду.
В десятичной системе счисления: число "десять" обозначается цифрами 1 и 0 -

.
В семеричной системе счисления: число "семь" обозначается цифрами 1 и 0 -

.
Числа по порядку:
Ноль -

и

Один -

и
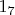
Два -

и

Три -

и

Четыре -

и

Пять -

и

Шесть -

и

Семь -

и

Восемь -

и

Девять -

и

Десять -

и

Одиннадцать -

и

Пока всё вроде ясно.
Далее привожу фрагмент из книги С.В. Фомина "Системы счисления" 1987 г. страницы 5-6

Приводится число "две тысячи пятьсот сорок восемь" -

и

Согласно формуле представления числа в виде суммы коэффициентов, умноженных на советующие степени основания системы счисления, получается так:


Вопрос: если в семеричной системе счисления число "семь" обозначается как

, то есть цифра "7" там вообще не используется, почему в формуле представления числа цифра "7" используется? Ведь по идее там должны быть цифры 1 и 0 (

):

Это и непонятно.