Доказать, что это число будет натуральным при любых натуральных
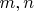
:

Идея, которая пришла в голову, но которую не знаю как реализовать: если заменить

на

, то это равносильно замене минуса на плюс под радикалами, и возможно, что при раскрытии скобок слагаемые также сократятся, как и при минусе.
Также удалось получить гипотезы для общих формул для нескольких

:

:


:


:


:


:

Есть идеи для общего случая?