И эта биекция появляется, тогда, когда мы определяем отношение эквивалентности

,

, где

, тогда элементу

ставится в соответствие множество вида

?
Пусть, например, у меня есть группа

, состоящая из множества чисел

определим групповую операцию, как:
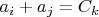
, очевидно, она абелева, выделим подгруппу

, тогда класс эквивалентности элемента

- это

?