Для нахождения простых чисел есть алгоритм, называемый решетом Эратосфена. Так как на форуме в последнее время активно обсуждались простые числа близнецы, то поразмыслив на эту тему получил алгоритм нахождения простых чисел близнецов. Возможно он тут и пригодится в связи с обсуждениями простых чисел близнецов.
Все пары простых-близнецов, кроме (3, 5), имеют вид

. Методом решета будут находиться эти числа

.
1. Выписать подряд все числа от 1 до некоторого числа

.
2. Взять первое число и получить числа p =

, для первого числа это числа

.
3. Зачеркнуть в списке числа от 6 до

считая шагами по p от

(это будут числа

, …) при

и соответственно (

, …) при

.
4. Зачеркнуть в списке числа от 4 до

считая шагами по p от

(это будут числа

, …) при

и соответственно (

, …) при

.
Для следующего числа

числа

это

.
Третий и четвертый шаги соответственно такие:
3. Зачеркнуть в списке числа от 13 до

считая шагами по p от

(это будут числа

, …) при

и соответственно (

, …) при

.
4. Зачеркнуть в списке числа от 9 до

считая шагами по p от

(это будут числа

, …) при

и соответственно (

, …) при

.
Повторять шаги 3 и 4 со следующими числами, пока возможно.
Все незачеркнутые числа в списке дают простые числа близнецы по формуле

.
Первое зачеркнутое число будет

и значит из четверки по формуле

не получить пару простых чисел близнецов, одно из чисел

соответственно делится только на

.
Следующее число

не перечеркивается шагами три и четыре и дает простые числа близнецы

.
Число

и также

, значит одно из чисел вида

делится на пять и на семь. Это число
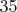
.
Число

другим способом не перечеркивается в списке, и значит одно из чисел 49 делится только на 7.