Конечность информации Фишера

[meshok]

Доброго времени суток!
Как можно расшифровать такую фразу: "известно, что информация Фишера вероятностной плотности f конечна, если у нее интегрируемы первые три производные."?
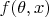
Моя предположение (рассматриваю самый простой случай, чтобы осталась лишь основная суть утверждения): Пусть дана функция двух переменных $f(\theta,x)$, которая при каждом фиксированном $\theta$ есть плотность распределения некоторой случайной величины. Если первые три производные $f'_\theta(\theta,x),f''_{\theta \theta}(\theta,x),f'''_{\theta\theta\theta}(\theta,x)$ интегрируемы по $x$ на $\mathbb{R}$ при каждом $\theta$, то информация Фишера

$$I(\theta)=\int \limits_{\mathbb{R}}\frac{1}{f(\theta,x)}\left(\frac{\partial f}{\partial \theta}(\theta,x)\right)^2dx$$

конечна при каждом $\theta$.
Попробовал найти какое-нибудь утверждение в таком же духе, но безрезультатно. Был бы очень благодарен за ссылку на данное утверждение.