Остаточные события в законе 0/1

[Plague Doctor]

Добрый день.

Пытаюсь разобраться с законом "нуля или единицы" и, видимо, мне не хватает понимания в теории множеств. К самому закону это относится опосредованно, но все-таки хотелось бы разобраться.
Имеем последовательность независимых одинаково распределенных бернуллиевских случайных величин
$\xi_{1}, \xi_{2}...$

$P\left\{ \xi_{i} = +1 \right\} = P\left\{ \xi_{i} = -1 \right\} = 1\slash2$

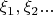
Есть классический пример остаточного множества со сходимостью ряда:
$A_{1} = \left\{ \omega \,\colon \sum\limits_{n=1}^{ \infty } \frac{ \xi_{n} }{ n } - \text{сходится} \right\}$

Тут, вроде как, все понятно, из чего это множество состоит - это множество последовательностей элементарных исходов, при которых ряд случайных величин сходится.


И далее, приводится еще ряд множеств, которые являются остаточными событиями. И вот тут я просто не понимаю, из чего они состоят. Может, вы подскажете.

1. $A_{2} = \left\{ \xi_n \in I_{n} \text{ б.ч.} \right\} =\varlimsup\limits_{n} \left\{ \xi_{n} \in I_{n} \right\}, I_{n} \in \mathscr{B} (R)$
Тут я не понимаю, что это за индикатор такой? И, соответственно, из чего будет состоять предельное множество.

2. $A_{3} = \left\{ \varlimsup\limits_{n} \xi_{n} < \infty \right\}$
Хз, что тут происходит, с учетом того, то хи принимает значения +1 или -1.
И что изменится, если заменить верхний предел на обычный?

3. $A_{4} = \left\{ \varlimsup\limits_{n} \frac{ \xi_{1} + ... + \xi_{n}}{ n } < \infty \right\}$
$A_{5} = \left\{ \frac{ S_{n}}{ n } - \text{сходится} \right\}$
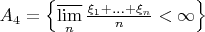
A4 и A5 - это не одно и то же? И они оба - не тоже самое, что и А1, за исключением знаменателя? Т.е. это не множество последовательностей элементарных исходов, сумма которых (поделенная на n) сходится?
И если заменить в А4 верхний предел на обычный, изменится ли "остаточность" множества?

4. $A_{6} = \left\{ \varlimsup\limits_{n} \frac{ \xi_{1} + ... + \xi_{n}}{ n } < c \right\}$
Чем в данном случае верхний предел отличается от просто предела, т.к. следующее множество не является остаточным (почему???):
$B_{1} = \left\{ \lim_{n}(\xi_{1} + ... + \xi_{n}) - \text{существует и меньше с} \right\}$

[Plague Doctor]

Plague Doctor в сообщении #1519269 писал(а):

Имеем последовательность независимых одинаково распределенных бернуллиевских случайных величин
$\xi_{1}, \xi_{2}...$

$P\left\{ \xi_{i} = +1 \right\} = P\left\{ \xi_{i} = -1 \right\} = 1\slash2$

Чего-то с этим я погорячился.
$\xi_{1}, \xi_{2}...$ - просто последовательность каких-то случайных величин.
Но ситуацию это все-равно не прояснило.

[marie-la]

Plague Doctor в сообщении #1519269 писал(а):

1. $A_{2} = \left\{ \xi_n \in I_{n} \text{ б.ч.} \right\} =\varlimsup\limits_{n} \left\{ \xi_{n} \in I_{n} \right\}, I_{n} \in \mathscr{B} (R)$

Тут какие-то множества имеются в виду, наверное. Например, $\xi_n=n$ бесконечно часто.

Plague Doctor в сообщении #1519269 писал(а):

2. $A_{3} = \left\{ \varlimsup\limits_{n} \xi_{n} < \infty \right\}$

Обычный предел может не существовать, как в вашем примере. Так что есть разница.

3. $A_{4} = \left\{ \varlimsup\limits_{n} \frac{ \xi_{1} + ... + \xi_{n}}{ n } < \infty \right\}$
$A_{5} = \left\{ \frac{ S_{n}}{ n } - \text{сходится} \right\}$

$A_5$ подмножество $A_4$.

Plague Doctor в сообщении #1519269 писал(а):

4. $A_{6} = \left\{ \varlimsup\limits_{n} \frac{ \xi_{1} + ... + \xi_{n}}{ n } < c \right\}$

Верхний предел может существовать, предел нет.
$B_1$ не принадлежит остаточной сигма-алгебре, поскольку зависит от первых величин - увеличьте $\xi_1$ и можете выйти из $B_1$.