Кострикин Введение в алгебру, часть 2, гл. 2, параграф 2, задача 5:
Доказать, что для люых линейных операторов

на

имеет место равенство:

И я туплю, наверное, но как это вообще может быть верно?

произвольны, а равенство несимметрично. По симметрии сразу получаем:
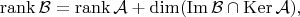
откуда

и

.
Или его можно опровергнуть так:
Пусть

. Возьмем такие операторы

и базис, что матрица

в нем равна

, а матрица

равна

. Тогда
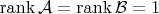
, а

,
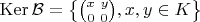
и

т.е. в итоге

.
Где я не прав?