Дана функция
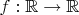
, причём

непрерывна в

.
Известно, что

. Требуется найти производную в

.
Я начал так:

И видно, что если повторять этот процесс до бесконечности, то получается геом. прогрессия, сумма которой есть

, чутьё подсказывает, что это правильный ответ, однако в моих рассуждениях не пропадает пресловутое

, что можно сделать?