В сообщении выражается предположение, что тензорное произведение может быть построено только из векторов-функций, но не из векторов-аргументов.
1.
Возьмем два взаимно сопряженных

-мерных векторных пространства

и

с базисом

в

и взаимным с ним базисом

в

.
Пусть

будет пространством векторов,

пространством линейных функций (пространством ковекторов) от векторов пространства

.
Тогда произвольный ковектор

имеет значения

на базисных векторах

, и значения эти равны его координатам

по базису

.
Так же и произвольный ковектор

имеет значения

на базисных векторах

, и значения эти равны его координатам

по базису

.
Пусть

два произвольных вектора пространства

.
Пусть

и

их разложения по базису

.
Возьмем линейные формы

и

и перемножим их:


Здесь

это аддитивная матрица (все элементы которой складываются).
Из нее можно выделить матрицу

билинейной формы

, возникшей при перемножении линейных форм

:

Если умножить ее на координаты векторов

по правилу перемножения матриц (

слева,

справа), то получим аддитивную матрицу

, которая равна билинейной форме

:

Поскольку

, матрица
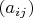
(матрица

) билинейной формы

может быть представлена как матрица

, причем матрица

получается в результате тензорного перемножения матриц линейных форм

(эти одномерные матрицы представляют собой координаты ковекторов

по базису

):

[Если перемножить две линейные комбинации, получить таким образом билинейную форму и выделить из нее матрицу попарных произведений базисных векторов, то можно затем произвольно назначить значения элементов этой матрицы.
Но если перемножить не линейные комбинации, а линейные формы, то значения элементов матрицы полученной билинейной формы произвольно назначить мы не можем, так как они уже есть -- это попарные произведения элементов (одномерных) матриц перемноженных линейных форм.]
Таким образом, в результате тензорного перемножения двух ковариантных тензоров первого ранга типа

, то есть ковекторов

, получается тензор второго ранга типа

-- дважды ковариантный тензор, то есть билинейная функция

:

что иначе можно иначе записать как

Из обеих этих записей видно, что

это функции, поскольку если бы они не были функциями, то, как я понимаю, из них нельзя было бы построить тензор (об этом ниже).
Кроме того, из обеих записей видно, что

это ковекторы: из первой -- по тому, что при

имеется обозначение

, которое указывает, что это дважды ковариантный и ни разу не контравариантный тензор, и потому тензоры, из перемножения которых он получился, могут быть только оба ковариантными, из второй -- по нижнему положению индексов.
2.
Пока что рассматривалось тензорное произведение не векторов, а ковекторов, и именно потому, что пространство

, то есть пространство ковекторов, было объявлено пространством функций.
Я, вообще, не вижу, как можно было бы построить тензорное произведение из векторов, которые не являются функциями, по крайней мере, я нашел только, как построить его из векторов-функций.
Однако, если посмотреть на функции как на векторы -- и назвать их так, -- можно говорить о построении тензорного произведения из векторов, имея, тем не менее, в виду, что они являются функциями.
Так и делается: поскольку пространство векторов и сопряженное с ним пространство функций "равноправны", говорят не только: "функция от вектора", - но и: "вектор от функции", -- разумея в последнем случае, что "вектор" это функция, а "функция" -- вектор.
Это хорошо видно из описания построения тензорного произведения в "Алгебре" ван дер Вардена
https://scask.ru/d_book_alg.php?id=28 (думаю, что это она, хотя об этом можно только догадываться: на этом сайте почти никогда нельзя точно узнать, что за книга и кто ее написал).
Почти сразу же автор говорит:
Цитата:
Из двух векторов

и

можно следующим образом построить тензорное произведение

и через несколько слов становится ясно, что векторы он считает функциями, а ковекторы аргументами.
Построение у него то же, что у меня -- вероятно, потому что другого и быть не может, -- только наоборот: у меня основное пространство это пространство аргументов, а сопряженное -- пространство функций, -- даже обозначения почти те же (из этого можно предположить, что сначала я прочитал его описание, а потом написал свое, но это не так, просто имеет место какое-то удивительное совпадение).
Я хочу сказать, что -- как я думаю, -- не бывает тензорного произведения векторов-аргументов, бывает только тензорное произведение векторов-функций, и при этом получается тензор-функция более высокого ранга.
И это не удивительно: функции более высокого ранга строятся из функций более низкого ранга, -- скорее было бы удивительно, если бы удалось построить тензор-функцию из векторов, которые не являются функциями.
Первоначально функция это не вектор, а то, что воздействует на вектор, тогда вектор пассивный объект, а функция -- активный (хотя, конечно, все относительно), но после того, как обнаруживается, что на функции можно смотреть как на векторы, их начинают называть векторами.
Если под тензором понимать функцию, а не аргумент, то вектор является тензором не тогда, когда воздействуют на него, а тогда, когда воздействует он.
Вообще, по одному из определений тензор это полилинейная функция, так что каждый тензор это функция.
Однако множество всевозможных функций одного вида представляет собой линейное пространство, поскольку можно элементы этого множества складывать между собой и умножать на числа, и поэтому тензор может выступать также в роли аргумента -- когда функцию берут от него, то есть он может быть пассивным -- таким, на который воздействуют другие объекты.
Но строится он как функция -- и из функций.
Хотя, может быть, возможно построить пассивный тензор из векторов, которые не являются функциями?
3.
У меня было сложилось представление, что ковектор это вектор-функция, наверное, потому, что в учебниках, которые я читал, сопряженное пространство сначала представлялось как пространство функций.
Однако, это ошибочное представление. Ковектор это не обязательно функция, ковектор это элемент сопряженного пространства

(если пространство

, с которым оно сопряжено, считать основным), и называется он ковариантным вектором не потому, что он функция, а потому что его координаты при переходе от одного базиса основного пространства к другому (базису основного пространства) изменяются ковариантно этому переходу, является же он функцией или аргументом, зависит от выбора -- нашего или еще чьего-нибудь.
Возьмем аддитивную матрицу

которую можно представить в виде

Есть 4 варианта:
1)

(оба) -- функции, тогда

(оба) -- аргументы, этот случай мы разобрали в п.1;
2)

(оба) -- аргументы, тогда

(оба) -- функции;
3)

-- функция,

-- аргумент, тогда

-- аргумент,

-- функция;
4)

-- аргумент,

-- функция, тогда

-- функция,

-- аргумент.
Соответственно, из

можно выделить 4 в общем случае разных матрицы:
1)

,
2)

,
3)

,
4)

.
(В скобках стоят тензорные произведения координат функций.)
О том, что они разные можно судить хотя бы по их ведущим элементам

.
[При этом

представляет собой одно и то же число, независимо от того, какие векторы (ковекторы) из

являются аргументами, а какие функциями.]
1) Случай с матрицей

(обозначенной просто

) разобран в п.1.
2)

-- матрица билинейной функции

, то есть тензорного произведения контравариантных векторов

:

Для того, чтобы построить его, надо посмотреть на векторы

как на функции, а на ковекторы

как на аргументы (то есть, как у ван дер Вардена, пространство

считать пространством аргументов, а пространство

пространством функций), и в свете этого провести рассуждения п.1.
3)

-- матрица билинейной функции

, то есть тензорного произведения ковариантного вектора

и контравариантного вектора

:

4)

-- матрица билинейной функции

, то есть тензорного произведения контравариантного вектора

и ковариантного вектора

:

3) и 4), хотя и разные, но каждая из них -- матрица билинейной функции один раз ковариантной и один раз контравариантной, возьмем одну их них --

.
Чтобы построить соответствующее ей тензорное произведение, надо посмотреть на вектор

и ковектор

как на функции, а на ковектор

и на вектор

как на аргументы, и в свете этого провести рассуждения п.1.
В этом случае каждый элемент, как пространства

, так и пространства

, может выступать в роли и аргумента, и функции, в зависимости от ситуации: после того, как выбраны в качестве функций и тензорно перемножены вектор

и ковектор

, могут выбираться в качестве аргументов для полученной билинейной функции

произвольные пары элементов по одному из каждого пространства

(в том числе и ковектор

и вектор

-- каждый в своей паре или в одной паре), то есть матрица

может умножаться на координаты элементов каждой такой пары -- на строку координат ковектора слева и на столбец координат вектора справа.