Универсальное свойство прямой суммы групп

[Padawan]

Пусть $\{G_i\}_{i\in I}$ -- семейство групп. Назовем их прямой суммой $\bigoplus\limits_{i\in I} G_i$ подмножество декартова произведения $\prod\limits_{i\in I} G_i$, состоящее из всех наборов $(g_i)_{i\in I}$ у которых $g_i\neq e$ только для конечного числа индексов. Операция определяется покоординатно: $(g_i)_{i\in I}\cdot (g'_i)_{i\in I}=(g_ig'_i)_{i\in I}$.
Для любого $j\in I$ пусть $\mathrm{in}_j\colon G_j\to \bigoplus\limits_{i\in I} G_i$ -- вложения, то есть $\mathrm{in}_j (g_j)=(g_i)_{i\in I}$, где $g_i=e$ при $i\neq j$. Это иньективные гомоморфизмы.
Утверждение. Для любой абелевой группы $(\Gamma,+)$ и любого набора гомоморфизмов $f_i\colon G_i\to \Gamma$ существует единственный гомоморфизм $f\colon \bigoplus\limits_{i\in I} G_i\to\Gamma$ такой, что $f_i=f\circ \mathrm{in}_i$ для всех $i\in I$.
Доказательство. Заметим, что элементы множеств $\mathrm{in}_i (G_i)$ и $\mathrm{in}_j (G_j)$ при $i\neq j$ перестановочны. Для любого элемента $(g_i)_{i\in I}$ выберем конечное множество $I_0\subset I$ такое, что $g_i=e$ при $i\in I\setminus I_0$, и положим $f((g_i)_{i\in I})=f\left(\prod\limits_{i\in I_0} \mathrm{in}_i(g_i)\right)=\sum\limits_{i\in I_0} f\circ\mathrm{in}_i(g_i)=\sum\limits_{i\in I_0} f_i(g_i)$ (доказана единственность). Понятно, что от выбора множества $I_0$ значение $f((g_i)_{i\in I})$ не зависит. Покажем, что $f$ есть гомоморфизм из $\bigoplus\limits_{i\in I} G_i$ в $\Gamma$. Пусть $(g_i)_{i\in I}, (g'_i)_{i\in I}\in\bigoplus\limits_{i\in I} G_i$. Выберем множество $I_0\subset I$ такое, что $g_i=e$ и $g'_i=e$ при всех $i\in I\setminus I_0$. Тогда

$$ f((g_i)_{i\in I}\cdot (g'_i)_{i\in I})=f((g_ig'_i)_{i\in I})=\sum\limits_{i\in I_0} f_i(g_ig'_i)= \sum\limits_{i\in I_0} (f_i(g_i)+f_i(g'_i))=(\text{абелевость } \Gamma)=$$ $$ =\sum\limits_{i\in I_0} f_i(g_i)+\sum\limits_{i\in I_0} f_i(g'_i)=f((g_i)_{i\in I})+f((g'_i)_{i\in I}) $$

Это правильно? А то я считал, что указанное свойство выполняется только для абелевых групп $\{G_i\}_{i\in I}$. Но в приведенном доказательстве вроде бы используется только абелевость группы $\Gamma$. Получается, что для любых групп $G_1$, $G_2$ характеры (т.е. гомоморфизмы в единичную окружность в комплексной плоскости) группы $G_1\times G_2$ есть в точности произведения характеров групп $G_1$ и $G_2$? То есть $\chi((g_1,g_2))=\chi(g_1)\chi(g_2)$?

[vpb]

Padawan в сообщении #1515703 писал(а):

Это правильно?

Правильно.

Padawan в сообщении #1515703 писал(а):

Получается, что для любых групп $G_1$, $G_2$ характеры (т.е. гомоморфизмы в единичную окружность в комплексной плоскости) группы $G_1\times G_2$ есть в точности произведения характеров групп $G_1$ и $G_2$? То есть $\chi((g_1,g_2))=\chi(g_1)\chi(g_2)$?

Тоже верно.

Следует также упомянуть, для общего образования, вот что. Декартово произведение $P=\prod_{i\in I}G_i$ (которое без условия конечности, т.е. нет условия, что в наборе $(g_i\in G_i\mid i\in I)\in P$ лишь конечное число компонент отлично от нуля), вместе с гомоморфизмами проекции $\pi_i\colon P\to G_i$, является произведением в категории групп в следующем смысле: для любых гомоморфизмов $\alpha_i\colon X\to G_i$, где $X$ --- какая-то группа, существует и единственен гомоморфизм $\beta\colon X\to P$ такой, что $\alpha_i=\pi_i\circ\beta$ для всех $i\in I$. 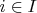Есть также копроизведение, т.е. группа $Q=\coprod_{i\in I}G_i$ и семейство гомоморфизмов $\sigma_i\colon G_i\to Q$ такие, что для любого семейства гомоморфизмов $\alpha_i\colon G_i\to X$ существует и единственен гомоморфизм $\beta\colon Q\to X$ такой, что $\alpha_i=\beta\circ\sigma_i$ для всех $i\in I$. 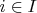Копроизведение можно описать в групповых терминах, а именно --- это т.наз. свободное произведение семейства групп.

В категории же абелевых групп копроизведение --- это прямая сумма. (Но, копроизведение семейства абелевых групп в категории абелевых групп и копроизведение того же семейства в категории всех групп, т.е. их свободное произведение --- разные вещи ! Второе вообще неабелево, если групп больше одной.)

[Padawan]

vpb
Спасибо! Про произведения-копроизведения знаю. Просто я думал, что именно в абелевых группах надо прямую сумму рассматривать. А начал доказывать - и вот, абелевость только $\Gamma$ нужна!

[vpb]

На здоровье !