Может быть полезнее всё наоборот свести в кватернионы:

, так что мы интегрируем

по

. Переназвал свой

в

, чтобы не путался с вашими обозначениями. Если записать скалярное произведение не с минусом, а через сопряжение (которое для векторных кватернионов и есть минус):

— и вспомнить

, то множитель произведения примет вид

, что выглядит подозрительно. Это «скалярное произведение»

и

, где для произвольных кватернионов оно будет равно уже

, то есть мы получили обычное евклидово скалярное произведение в четырёхмерном пространстве.
Если

, где

— угол поворота и

— ось поворота,

, то тот множитель превратится во что-то такое:

Нет, зря вы их назвали

— в глазах рябит немного, лучше бы
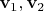
.
Тройное произведение

тут единственное слагаемое, которое сменит знак, если поменять

местами. Таким образом, среднее его самого по себе должно быть нулевым. Зато когда

, оно может давать какой-то вклад. Страшную скобку при

можно записать просто как

, но вряд ли это упростит дела.
Когда мы интегрируем в таком виде,

уже равномерно распределена по обычной двумерной сфере, а вот

будут так же хитры как

выше.
Мне думается, эти советы все какие-то не в ту сторону, или интеграл воистину сложно брать.
-- Чт апр 01, 2021 19:37:47 --madschumacherВот что вы на это скажете — страшно? Ещё пробовал интуитивно выдумать формулу для произвольного

, глядя на ваши найденные случаи

, но как-то не выстраивается. И например даже если разделить на случаи чётного и нечётного

, то ноль не вяжется с тройным произведением (хотя совершенно ясно, что при

разумеется должен быть ноль).