Magnetic Resonance Imaging Physical Principles and Sequence Design Second Edition By Robert W. Brown et. all © 2014 byJohn Wiley & Sons, Inc.
Problem 7.9
Цитата:
Investigate the effect of using different combinations of rf systems to tip the spins and measure the resulting signal.
a) Assume two identical spins are excited by a uniform field, such that they both receive a perfect
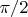
-rotation into the transverse plane. What will be the relative difference in the signal between the two spins if
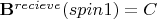
, a constant, and
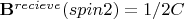
?
b) Assume now that the two spins from (a) are excited by different transmit fields. The first spin experiences
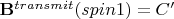
, another constant, and receives a
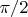
flip. The second spin only experiences a field of
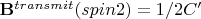
, and therefore is not rotated by the same angle. If
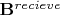
is identical for the two spins, what is the relative difference in their measured signal?
c) It appears from the preceding problems that if only one of the transmit and receive fields is inhomogeneous, but not both, then it might be best to transmit with an inhomogeneous rf field, and receive with a homogeneous field. However, this is not how experiments are normally performed. Explain why this might be the case. Hint: Recall that the received signal depends upon
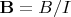
and preview Ch. 15.
Насколько я понял, если принебречь вопросами релаксации и рассаотреть амплитуду получаемого сигнала, то она описывается формуло (7.31)
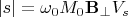
.
a)
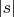
линейно зависит от
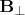
, таким образом отношение
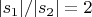
.
b) С отличием в
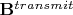
получается несколько другая история. Угол переворота определяется формулой (3.31)
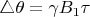
.
Если
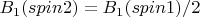
, то и угол
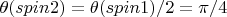
. Тогда проекция
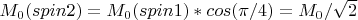
таким образом отношение
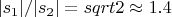
Из задач a) и b) cледует, что на отношение сигнало сильнее влияет неоднородность
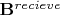
[/math].
Это описывается в абзаце к задаче c).
Цитата:
It appears from the preceding problems that if only one of the transmit and receive fields is inhomogeneous, but not both, then it might be best to transmit with an inhomogeneous rf field, and receive with a homogeneous field. However, this is not how experiments are normally performed. Explain why this might be the case. Hint: Recall that the received signal depends upon
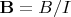
and preview Ch. 15.
Но я не совсем понимаю, что хотят в третье задачи. Посмотрел главу 15. Подсказок не увидел.
Цитата:
Explain why this might be the case.
Подскажите на что намекают авторы?