Ортогональная матрица, степень которой равна единичной

[val812elf]

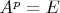
Каков общий вид вещественных ортогональных матриц $n$-го порядка, удовлетворяющих условию $A^p=E$, где $p$ - заданное натуральное число, $E$ - единичная матрица?

Как я вижу, в случае $p=2$ мы имеем: $A^2=E$, откуда $A^{-1}=A$, далее по определению ортогональности $A^T=A^{-1}$, откуда $A^T=A$, то есть $A$ - симметричная матрица.

А что можно сказать про общий вид таких матриц например для $p=5$ или $p=8$ ? Можно ли указать этот общий вид?

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- отсутствуют собственные содержательные попытки решения задачи.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.