Минимальная скорость для преодоление горки

[letoo]

EUgeneUS в сообщении #1508731 писал(а):

а) понять, откуда взялось $\Delta E$ и выразить его через $v$ и $u$. Подставлять ранее найденное $v$ пока не нужно, чтобы не загромождать красоту лишними деталями.
б) проделать всё тоже самое с импульсом.

1)$\Delta E=\frac{m(V+2u)^2}{2}-\frac{mv^2}{2}$(это изменение энергии от столкновение с стенкой)
2)$\Delta p=m(v+2u)-mv$

[EUgeneUS]

letoo в сообщении #1508741 писал(а):

1)$\Delta E=\frac{m(V+2u)^2}{2}-\frac{mv^2}{2}$(это изменение энергии от столкновение с стенкой)

$v$ - это скорость шайбе перед ударом со стеной. А что такое $V$?

letoo в сообщении #1508741 писал(а):

2)$\Delta p=m(v+2u)-mv$

Это неверно.
Импульс это вектор. У нас задача одномерная, но это не повод игнорировать знаки у проекции на единственную ось.
ЗСИ тоже надо записать.

[letoo]

EUgeneUS в сообщении #1508745 писал(а):

letoo в сообщении #1508741 писал(а):

1)$\Delta E=\frac{m(V+2u)^2}{2}-\frac{mv^2}{2}$(это изменение энергии от столкновение с стенкой)

$v$ - это скорость шайбе перед ударом со стеной. А что такое $V$?

letoo в сообщении #1508741 писал(а):

2)$\Delta p=m(v+2u)-mv$

Это неверно.
Импульс это вектор. У нас задача одномерная, но это не повод игнорировать знаки у проекции на единственную ось.
ЗСИ тоже надо записать.

1) Вместо $V$ должно быть $v$(опечатался)
2) ЗСИ после отскока до поднятие шайбы до вершины горки $mv_1=(m+M)v_2$
Насчёт изменения импульса $\Delta p_x=m(v+2u)+mv$ ось: ox по движению плиты

[EUgeneUS]

letoo в сообщении #1508748 писал(а):

2) ЗСИ после отскока до поднятие шайбы до вершины горки $mv_1=(m+M)v_2$

Неверно. Напоминаю, мы рассматриваем самое начальное и самое конечное состояние.

В начальном состоянии в ЛСО импульс равен нулю (горка и шайба покоятся), потом дают пинка ($\Delta p_x$), и в конечном состоянии горка с шайбой двигается со скоростью $v_2$.
Теперь нужно всё собрать в кучу, избавиться от $v_2$ и выразить $u$ через $v$.
Вы будете удивлены простоте результата.

(Оффтоп)

впрочем, зная ответ понятно, что получится очень просто.

[letoo]

EUgeneUS в сообщении #1508752 писал(а):

Теперь нужно всё собрать в кучу, избавиться от $v_2$ и выразить $u$ через $v$.

Получилось красиво. $Mu=mv$. Получается, что для того чтобы шайба после отскока поднялась на туже высоту, необходимо чтобы скорость плиты равнялась скорости горки.

[EUgeneUS]

letoo в сообщении #1508757 писал(а):

$Mu=mv$.

Дальше совсем просто. Подставляем полученное ранее $v$, получаем верный ответ. Надеюсь, Вы это сделали.

letoo в сообщении #1508757 писал(а):

Получается, что для того чтобы шайба после отскока поднялась на туже высоту, необходимо чтобы скорость плиты равнялась скорости горки.

Скорости горки, после того как с неё съехала шайба, надо полагать.
Равна по модулю и противоположна по направлению.
Это очень наглядно видно в ИСО стены.

Разберем этот вариант решения, там есть несколько поучительных моментов.
1. Записываем ЗСИ для начально и конечного состояния, ось $Ox$ - как у Вас, справа налево, если смотреть на рисунок.
$-(M+m) u + \Delta p_x = (M+m) v_2$

2. Записываем ЗСЭ для начально и конечного состояния:
$\frac{(M+m) u^2}{2}+ \Delta E = \frac{(M+m) v_2^2}{2}$

Но в этой ИСО $\Delta E=0$, так как стена покоится и дополнительной энергии взяться не откуда.
Поэтому сразу: $u^2 = v_2^2$
С другой стороны, $\Delta p_x \ne 0$, поэтому
а) $u \ne v_2$, это может быть только в одном случае: $u = -v_2$, то есть после всех пертрубаций в ИСО стены горка и шайба двигаются со скоростью, которая равна по модулю начальной ($u$), но противоположна направлена.
б) То есть импульс всей системы меняется на противоположный. Но и удар шайбы об стену меняет импульс шайбы на противоположный. А значит шайба "должна утащить с собой" весь импульс системы, поменять его знак при ударе и притащить обратно. Поэтому сразу вывод: после того, как шайба съехала с горки, импульс горки равен нулю, она будет покоиться относительно стены, пока шайба не вернётся.

Избавимся от $v_2$ и сложим одинаковые члены: $\Delta p_x = 2 (M+m)u$
Далее, чтобы получить ответ, нужно найти $\Delta p_x$.
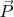
Можно, конечно, посчитать его заново в ИСО стены, но зачем? Воспользуемся фактом, что $\Delta \vec{P}$ является инвариантом при переходах между ИСО, и используем $\Delta p_x$ уже найденное в ЛСО. ($E$, $\Delta E$, $\vec{P}$ инвариантами не являются!)

letoo в сообщении #1508748 писал(а):

$\Delta p_x=m(v+2u)+mv$

Откуда:
$2m(v+u) = 2 (M+m)u$, и получается волшебное $m v = M u$

[EUgeneUS]

UPD: выше был несколько неаккуратен со знаками:
а) нужно либо в ЗСИ убрать минус перед первым слагаемым слева (тогда $u$ и $v$ рассматриваются, как обозначение проекций соответствующих скоростей на $Ox$).
б) либо получается $u = v$, без минуса (тогда $u$ рассматриваются, как величина модуля проекции $u$ на $Ox$).

[Dan B-Yallay]

EUgeneUS в сообщении #1508783 писал(а):

Разберем этот вариант решения, там есть несколько поучительных моментов.

А можно ли проще?

Пусть шайба ($m$) соскользнула с горки ($M$) и они движутся в разные стороны со скоростями $v$ и $ v_0$ соответственно. То есть $mv = Mv_0$. Тогда если их направить с теми же скоростями (по модулю) но уже навстречу друг другу, то шайба заберется на горку. В СО, которая движется влево согласно рисунка со скоростью $2v_0$ горка как раз едет навстречу шайбе с нужной скоростью. А для шайбы (после отражения от стенки и движyщейся со скоростью $v+2u$) имеем уравнение:

$$v +2u - 2v_0 = v$$

Вроде бы всё. Или я где-то смухлевал?

[EUgeneUS]

Dan B-Yallay в сообщении #1508913 писал(а):

А можно ли проще?

Подсчитал количество выкладок в каждом из вариантов.
И должен признать, что Ваш вариант проще в два раза.