Уравнение теплого баланса

[add314]

Решал задачу на уравнение теплого баланса (программа 10 класса). Условие такое:
После опускания в воду, имеющую температуру $t_{1}=10°C$, тела, нагретого до $t_{2}=100°C$, через некоторое время установилась общая температура $\Theta_{1}=40°C$. Какой станет температура воды (обозначил $\Theta_{2}$), если, не вынимая первого тела, в нее опустить еще одно такое же тело, нагретое до $t_{2}=100°C$?
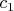
Сначала прочитал задачу неправильно, понял, якобы в воду при известной температуре $t_{1}$ положили во втором случае просто два тела температурой $t_{2}$ одновременно. В итоге получилась такая система (теплоемкость и массу воды обозначил соответсвенно $c_{1}$ и $m_{1}$, теплоемкость и массу тела - соответсвенно $c_{2}$ и $m_{2}$):

$$\left\{ \begin{array}{rcl} c_{1}\cdot m_{1}\cdot(\Theta_{1}-t_{1}) = c_{2}\cdot m_{2}\cdot(t_{2}-\Theta_{1})\\ c_{1}\cdot m_{1}\cdot(\Theta_{2}-t_{1}) = 2\cdot c_{2}\cdot m_{2}\cdot(t_{2}-\Theta_{2})\\ \end{array} \right.$$

Здесь я разделил и подствил числа, чтобы не париться (уравнения получались длинные).
Потом опомнился и составил уравнения уже правильно, по условию:

$$\left\{ \begin{array}{rcl} c_{1} \cdot m_{1} \cdot(\Theta_{1}-t_{1}) = c_{2} \cdot m_{2} \cdot (t_{2}-\Theta_{1}) \\ c_{1} \cdot m_{1} \cdot(\Theta_{2}-\Theta_{1}) = c_{2} \cdot m_{2} \cdot (t_{2}-\Theta_{2})-c_{2} \cdot m_{2} \cdot (\Theta_{2}-\Theta_{1}) \\ \end{array} \right.$$

Опять таки разделил, с формулами мучаться не стал, подставил числа.
Вопрос в чём. Дело в том, что в двух случаях получился один и тот же ответ, с ответом в задачнике совпадает ($\Theta_2 = 55°C$). Подскажите, то ли в решении ошибся где-то, хотя проверил несколько раз, то ли оба случая приводят к идентичному исходу, и не имеет значения опускать тела вместе или поочерёдно?

[Pphantom]

add314 в сообщении #1507269 писал(а):

Подскажите, то ли в решении ошибся где-то, хотя проверил несколько раз, то ли оба случая приводят к идентичному исходу, и не имеет значения опускать тела вместе или поочерёдно?

Оба случая приводят к идентичному результату, это нормально.

[realeugene]

Не имеет значения. В задачах на сохранение тепла при тепловом контакте различных тел это самое тепло можно считать некой сохраняющейся пропитывающей тела субстанцией, как когда-то думали, теплородом (только не говорите это слово на экзамене), которая распределяется между предметами в соответствии с их теплоёмкостями. В каком бы порядке ни соединять тела, в конечном состоянии конечная температура равна суммарному исходному количеству тепла делённому на суммарную теплоёмкость всех тел. В это нестрогом рассуждении предполагается, что при нулевой температуре и количество тепла нулевое, не имеет значения, что нулевая температура по шкале Цельсия.