Функции, сохраняющие рациональные точки

[AlexBS]

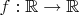
1) Пусть аналитическая функция $f: \mathbb{R}\to \mathbb{R}$ сохраняет рациональные точки, то есть $f(\mathbb{Q})\subset \mathbb{Q} $.
Верно ли, что $f(x)$ - рациональная функция с коэффициентами - рациональными числами?
2) Если про непрерывную (гладкую, аналитическую) функцию $f(x)$ известно только, что $f(\mathbb{Q}\setminus\{0\})\subset \mathbb{Q}, обязательно ли $f(0)\in\mathbb{Q} $?

КОММЕНТАРИИ. Это - не учебная задача, а исследовательская. Сформулированные в ней гипотезы возникли как обобщение следующей задачи (мною решённой):
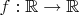
Пусть дифференцируемая функция $f: \mathbb{R}\to \mathbb{R}$ сохраняет рациональные точки и их знаменатели в следующем смысле: если $qx$ - целое число, то и $qf(x)$ - тоже целое число ($q\in\mathbb{N}, x\in \mathbb{R}$ - произвольны). Доказать, что $f(x)$ - многочлен с целыми коэффициентами степени 1 или ниже.

Есть ещё промежуточное обобщение (также решённое):
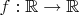
Пусть $k$ раз дифференцируемая функция $f: \mathbb{R}\to \mathbb{R}$ сохраняет рациональные точки, а их знаменатели - с точностью до кратной степени, в следующем смысле: если $qx$ - целое число, то и $q^kf(x)$ - тоже целое число ($q\in\mathbb{N}, x\in \mathbb{R}$ - произвольны). Доказать, что $f(x)$ - многочлен с целыми коэффициентами степени $k$ или ниже.

Следующий шаг обобщения - считать функцию $f(x)$ аналитической, сохраняющей рациональные точки (но не сохраняющей их знаменатели ни в каком смысле). Моя гипотеза состоит в том, что в таком случае $f(x)$ - рациональная функция с целыми (рациональными) коэффициентами.

Рациональность коэффициентов из рациональности функции вывести тоже не сложно, это я умею.

Осталось только из аналитичности доказать рациональность самой функции. Тут на ум приходит теорема из ТФКП, которая гласит, что всякое мероморфное (то есть, аналитическое с полюсами) отображение $\mathbb{C}P^1\to \mathbb{C}P^1$ является рациональным. Я не знаю, насколько этот путь перспективен - в моей задаче отображение задано на $\mathbb{R}$, мне не известно, есть ли обобщение этого факта на вещественно-аналитические отображения. Кроме того, нужно будет доказывать наличие полюса на бесконечности либо продолжаемость функции $f(x)$ в комплексную плоскость до мероморфной функции. У меня пока нет идей, как это можно сделать.

[Pphantom]

Тема перемещена из форума «Математика (общие вопросы)» в форум «Карантин»
по следующим причинам:

- отсутствуют собственные содержательные попытки ответа на вопросы.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Pphantom]

Тема перемещена из форума «Карантин» в форум «Математика (общие вопросы)»

[Padawan]

AlexBS в сообщении #1497843 писал(а):

1) Пусть аналитическая функция $f: \mathbb{R}\to \mathbb{R}$ сохраняет рациональные точки, то есть $f(\mathbb{Q})\subset \mathbb{Q} $.
Верно ли, что $f(x)$ - рациональная функция с коэффициентами - рациональными числами?
2) Если про непрерывную (гладкую, аналитическую) функцию $f(x)$ известно только, что $f(\mathbb{Q}\setminus\{0\})\subset \mathbb{Q}$, обязательно ли $f(0)\in\mathbb{Q}$?

Оба ответа отрицательные.
Можно построить аналитическую функцию $f\colon\mathbb R\to\mathbb R$ (даже аналитическую во всей комплексной плоскости) такую, что $f(\mathbb Q\setminus\{0\})\subset\mathbb Q$ и $f(0)=\sqrt2$.

Построение использует нумерацию $\{r_n\}_{n=0}^\infty$ всех точек из $\mathbb Q$, $r_0=0$, и последовательность $P_n(x)$ интерполяционных полиномов Лагранжа такую, что $P_n(r_k)=0$ при $0\leqslant k<n$. При этом $f(x)=\sum\limits_{n=0}^\infty c_nP_n(x)$, где коэффициенты $c_n$ выбираются с таким расчетом, чтобы ряд равномерно сходился на любом компактном подмножестве $\mathbb C$ (это обеспечит аналитичность). Детали построения предлагаю додумать самостоятельно.

[AlexBS]

Спасибо, это было мастерски! Дальнейшие детали ясны.