Как доказать, что предел существует?

[toofack]

Добрый вечер, решал задачу на днях: Даны числа $0 < a < b$. Последовательность $x_{n}$ задана начальным условием ${x_{1} = b}$ и соотношением $x_{2n} = \frac{x_{n} + a}{2}$
и $x_{2n+1} = \frac{x_{n} + \sqrt{ax_{n}} + a}{3}$ Имеет ли эта последовательность предел? Если имеет, то найдите его.

Решал так: Пусть предел существует и равен $x$, получается, что $ x = \frac{x+a}{2}$ $x = \frac{x + \sqrt{ax} + a}{3}$. Отсюда $2x = x + a$ и $3x = a + x + \sqrt{ax}$ Представим $3x = 2x + x \Rightarrow a + x + x = x + a + \sqrt{ax}$ Отсюда $x = a$

Правильное ли решение? Можете подсказать, как доказать, что предел существует, то есть нужно, доказать, что последовательность возрастает (убывает) и ограничена, я пытался мат индукцией, у меня не получилось, видать, плохо старался.

[mihaild]

toofack в сообщении #1497785 писал(а):

зная что ${x_{1} = b}$, получается, что $ x = \frac{b+a}{2}$

Каким образом вы это получили?

[toofack]

mihaild в сообщении #1497788 писал(а):

toofack в сообщении #1497785 писал(а):

зная что ${x_{1} = b}$, получается, что $ x = \frac{b+a}{2}$

Каким образом вы это получили?

Ошибся, сейчас исправлю

[mihaild]

Напишите рекурренты для $y_n = x_n - a$.

[toofack]

mihaild в сообщении #1497790 писал(а):

Напишите рекурренты для $y_n = x_n - a$.

Это поможет доказать убывание последовательности? Под рекуррентами вы имеете в виду рекуррентные соотношения?

[mihaild]

toofack в сообщении #1497792 писал(а):

Это поможет доказать убывание последовательности?

Очевидно что $x_n \to a \Leftrightarrow y_n \to 0$.

toofack в сообщении #1497792 писал(а):

Под рекуррентами вы имеете в виду рекуррентные соотношения?

Да. Получившиеся выражения будут проще, чем для $x_n$, может быть с ними станет очевидно, как доказывать сходимость.

[vpb]

toofack в сообщении #1497785 писал(а):

Решал так: Пусть предел существует и равен $x$, получается, что $ x = \frac{x+a}{2}$ $x = \frac{x + \sqrt{ax} + a}{3}$. Отсюда $2x = x + a$ и $3x = a + x + \sqrt{ax}$ Представим $3x = 2x + x \Rightarrow a + x + x = x + a + \sqrt{ax}$ Отсюда $x = a$

Если мы предположили, что предел существует, то достаточно одного соотношения $x = \frac{x+a}{2}$, остальное лишнее. Проблема в том, чтобы доказать, что он существует.

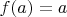
Предлагаю, в качестве первого шага, самостоятельно доказать следующее. Пусть $f$ --- функция, непрерывная, возрастающая, и такая, что $f(a)=a$ и $f(x)<x$ при $x>a$. Пусть $b>a$ --- любое число, и определим последовательность как $x_1=b$, $x_{n+1}=f(x_n)$. Доказать, что она сходится к $a$.