Доказательство ВТФ

[falconer]

Уважаемые участники и гости форума, предлагаю Вашему вниманию доказательства Великой теоремы Ферма.
Соколов Николай Алексеевич.


Лемма 1.

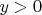
Для всех действительных $x>0$, $y>0$ и всех натуральных $n>1$ уравнение

$$ x^n + y^n = z^n\qquad(1) $$

имеет действительные решения. И в каждом таком решении должно выполняться неравенство

$$ 1<\frac{x+y}{z}\le\sqrt[n]{2^{n-1}}$$

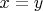
Для всех $x=y$ ответ очевиден: из

$$ 2x^n=2y^n=z^n$$

следует

$$ \frac{x}{z}=\frac{y}{z}=\frac{1}{\sqrt[n]{2}}=\frac{\sqrt[n]{2^{n-1}}}{2}$$

или

$$ \frac{x+y}{z}=\sqrt[n]{2^{n-1}}\qquad(2) $$

Перейдем к решениям, в которых $x \not= y$. Согласно коммутативности операции сложения решения уравнения (1), в которых $x<y$ и $x>y$, попарно связаны. Для каждого решения уравнения (1) ($a < b,c$), тройка чисел ($b,a,c$) также будет решением и наоборот. Поэтому, не теряя общности, можно анализировать только решения, в которых $x<y$.
С одной стороны, в любом решении уравнения (1) должны выполняться условия $x<z$ и $y<z$. Действительно, если, например, $x\ge z$, то $x^n\ge z^n$ и тем более $x^n+y^n > z^n$. Следовательно, в любом решении выполняется неравенство $x+y<2z$.
С другой стороны, в любом решении уравнения (1) $x+y>z$. Это становится очевидным, если записать уравнение в виде

$$ \left(x+y\right)^n-z^n=\sum_{i=1}^{n-1} \tbinom{n}{i} x^{n-i} y^i>0$$

Итак, в любом решении уравнения (1) выполняется неравенство

$$1 < \frac{x+y}{z} < 2$$

Правый предел в этом неравенстве можно уточнить.
Разделим уравнение (1) на $z^n$

$$\frac{x^n}{z^n}+\frac{y^n}{z^n}=1$$

Очевидно, что $1/2$ является центром отрезка $\left[x^n/z^n,\,y^n/z^n\right]$. Следовательно, для всех решений, в которых $x<y$, можем записать

$$ \frac{1}{2}-\frac{x^n}{z^n}=\delta=\frac{y^n}{z^n}-\frac{1}{2}$$

Извлечем корень степени $n$ из чисел $x^n/z^n,\,y^n/z^n$ и $1/2$. Величина $1/\sqrt[n]{2}$ уже не является центром отрезка $\left[x/z,y/z\right]$.
Докажем, что в любом решении уравнения (1), в котором $x<y$,

$$ \left(\delta_x=\frac{1}{\sqrt[n]{2}} - \frac{x}{z}\right) > \left(\delta_y=\frac{y}{z}-\frac{1}{\sqrt[n]{2}}\right)$$

Это следует из сравнения следующих величин

$$ \frac{\delta}{\delta_x}=\frac{1/2-x^n/z^n}{1/\sqrt[n]{2} - x/z}= \frac{1}{\sqrt[n]{2^{n-1}}}+\sum_{i=1}^{n-1} \frac{x^i}{z^i\sqrt[n]{2^{n-1-i}}}$$

$$\frac{\delta}{\delta_y}=\frac{y^n/z^n-1/2}{y/z-1/\sqrt[n]{2}}= \frac{1}{\sqrt[n]{2^{n-1}}}+\sum_{i=1}^{n-1} \frac{y^i}{z^i\sqrt[n]{2^{n-1-i}}}$$

Из $x<y$ следует, что $\delta/\delta_x<\delta/\delta_y$ и $\delta_x>\delta_y$. Следовательно,

$$ \frac{1}{2}\left(\frac{x}{z}+\frac{y}{z}\right) < \frac{1}{\sqrt[n]{2}}$$

или

$$ \frac{x+y}{z}<\sqrt[n]{2^{n-1}}$$

Итак, в любом решении уравнения (1), в котором $x \not= y$, должно выполняться неравенство

$$ 1<\frac{x+y}{z}<\sqrt[n]{2^{n-1}}\quad (3)$$

Объединяя (2) и (3), получаем: в любом решении уравнения (1) должно выполняться неравенство

$$ 1<\frac{x+y}{z}\le\sqrt[n]{2^{n-1}}\quad (4)$$

Лемма доказана.


Доказательство Великой теоремы Ферма.

Великая теорема Ферма (ВТФ) утверждает, что

Уравнение

$$x^n + y^n = z^n \qquad\qquad\qquad (5)$$

не имеет решений в натуральных числах для любого натурального $n > 2$.


При решении уравнения (5) можно ограничиться случаем, когда $x,y$ и $z$ являются взаимно простыми числами. Очевидно, если есть решение для взаимно простых $(x_1,y_1,z_1)$, то тройка $(d\cdot x_1,d\cdot y_1,d\cdot z_1)$ также будет решением при любом натуральном $d$.

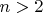
Нет необходимости доказывать ВТФ для всех показателей степени $n>2$. Достаточно доказать, что уравнение (5) не имеет натуральных решений для $n=4$ и $n=p$, где $p$ -- любое нечетное простое число.

Если ВТФ верна для $n=4$, то она верна и для любого показателя степени, кратного 4-м.

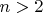
А все остальные показатели степени $n>2$ и не кратные 4-м, -- это все нечетные числа и все четные числа типа $2m$, где $m>1$ -- любое нечетное натуральное число.

Все эти числа имеют общее свойство. Их каноническая форма обязательно содержит хотя бы одно нечетное простое число. Следовательно, если ВТФ верна для любого простого показателя степени $p>2$, то она верна и для любого не кратного 4-м показателя степени.

Для $n=4$ ВТФ доказана Ферма. Для полноты картины приведем другое доказательство.

Для этого достаточно исходное уравнение

$$ x^4+y^4=z^4\qquad \qquad\qquad (6)$$

записать в виде

$$ \left(x^2+y^2-z^2\right)\left(x^2+y^2+z^2\right)=2x^2y^2 $$

Разделив обе части уравнения на $2x^2y^2$, получим

$$ \left(\frac{x^2+y^2-z^2}{2xy}\right)\left(\frac{x^2+y^2+z^2}{xy}\right)=1\qquad (6a)$$

Из (6а) видно, что равенство возможно лишь тогда, когда обе скобки слева являются взаимно обратными величинами, следовательно, должно выполнятся равенство

$$ \frac{b}{a}=b^2 $$

Здесь для краткости буквами $a$ и $b$ обозначены первая и вторая скобки соответственно.
Но

$$ \frac{b}{a}=\frac{2\left(x^2+y^2+z^2\right)}{x^2+y^2-z^2}\not= b^2=\frac{\left(x^2+y^2+z^2\right)^2}{x^2y^2}$$

Следовательно, ни при каких натуральных $x,y,z$ равенство (6a) не выполняется. Что и доказывает: уравнение (6) не имеет натуральных решений.

Кстати, использованный прием позволяет доказать более сильное утверждение: уравнение

$$ x^4+y^4=z^2$$

также не имеет натуральных решений. Для этого достаточно преобразовать его к виду

$$ \left(\frac{x^2+y^2-z}{2xy}\right)\left(\frac{x^2+y^2+z}{xy}\right)=1$$

Перейдем к доказательству ВТФ для всех простых показателей степени $p>2$.

$$ x^p + y^p = z^p \qquad\qquad (7)$$

Для любого нечетного простого $p$ левая часть уравнения (7) разлагается на множители

$$\left(x+y\right)\sum_{i=0}^{p-1} \left(-1\right)^i\,x^{p-1-i}y^i = z^p\qquad (8)$$

Допустим, что существует натуральное решение уравнения (7). Тогда согласно (8)
в этом решении сумма $x+y$ должна делить $z^p$. Но это невозможно.

С одной стороны, $(x+y)$ не может делить $z$, поскольку согласно лемме 1 в любом решении сумма
$(x+y)>z$. С другой стороны, из той же леммы следует, что в любом решении

$$ \frac{x+y}{z}<\sqrt[p]{2^{p-1}}$$

и, следовательно, наибольший общий делитель $x+y$ и $z$

$$ 1\le(x+y,z)<z$$

Т.е., $x+y$ не является делителем $z^p$.

Допустив наличие натурального решения, мы пришли к противоречию, которое доказывает: допущение было ошибочным, уравнение (7) не имеет натуральных решений.

ВТФ доказана.

[mihaild]

Первая замеченная мной ошибка - в строке

falconer в сообщении #1496480 писал(а):

$$ \frac{b}{a}=\frac{2\left(x^2+y^2+z^2\right)}{x^2+y^2-z^2}\not= b^2=\frac{\left(x^2+y^2+z^2\right)^2}{x^2y^2}$$

Это неравенство не обосновано.
(еще замечу, что вы заодно "доказали" ВТФ для $n = 2$, а так же для вещественных $x, y, z$)

[mihiv]

falconer в сообщении #1496480 писал(а):

С одной стороны, $(x+y)$ не может делить $z$, поскольку согласно лемме 1 в любом решении сумма
$(x+y)>z$. С другой стороны, из той же леммы следует, что в любом решении

$$ \frac{x+y}{z}<\sqrt[p]{2^{p-1}}$$

и, следовательно, наибольший общий делитель $x+y$ и $z$

$$ 1\le(x+y,z)<z$$

Т.е., $x+y$ не является делителем $z^p$.

Откуда это следует? Пусть $z=dk, (k,d-$ взаимно просты), а $x+y=d^p$, Тогда $(x+y,z)=d<z$, но $z^p$ делится на $x+y$.

[falconer]

Ответ на сообщение mihaild.

Я новичок на форуме. Пытался исправить текст своего сообщения. Не получилось. Вношу исправления здесь.

Относительно уравнения $x^4+y^4=z^4$. Текст, начиная со слов ''Для этого достаточно записать уравнение (6) в виде''
до слов ''Перейдем к доказательству ВТФ для всех простых показателей степени...''', заменить на следующий

Для этого достаточно записать уравнение

$$x^4+y^4=z^4\qquad(6)$$

в виде

$$ \left[\left(x+y\right)^2-z^2-2xy\right]\left[\left(x+y\right)^2+z^2-2xy\right]=2x^2y^2$$

Из последнего равенства видно, что в любом натуральном решении правая часть кратна $x^2y^2$, а левая может быть кратна $x^2y^2$ только в том случае, если

$$xy\;\left|\;\left[(x+y)^2-z^2\right] \text{ и } xy\; \right|\;\left[(x+y)^2+z^2\right]$$

Т.е., если $xy$ является делителем $z^2$, что противоречит условию теоремы: $x,y,z$ -- взаимно простые числа.

Полученное противоречие доказывает, что уравнение (6) не имеет натуральных решений.

Кстати, использованный прием позволяет доказать, что и уравнение

$$ x^4+y^4=z^2$$

также не имеет натуральных решений. Для этого достаточно преобразовать его к виду

$$ \left[\left(x+y\right)^2-z-2xy\right]\left[\left(x+y\right)^2+z-2xy\right]=2x^2y^2$$

А в связи с ''(еще замечу, что вы ..., а так же для вещественных $x, y, z$)'', заменяю текст, начинающийся со слов
'' Допустим, что существует натуральное решение уравнения (7).'' и до конца , заменяю на следующий

Допустим, что существует решение уравнения (7): тройка взаимно простых натуральных чисел $x=a,y=b,z=c$. Тогда согласно (8)
в этом решении сумма $a+b$ должна делить $c^p$. Но это невозможно.

С одной стороны, $(a+b)$ не может делить $c$, поскольку согласно лемме 1 в любом решении сумма
$(a+b)>c$. С другой стороны, из той же леммы следует, что в любом решении

$$\frac{a+b}{c}<\sqrt[p]{2^{p-1}}$$

и, следовательно, наибольший общий делитель $a+b$ и $c$

$$1\le(a+b,c)<c$$

Т.е., $a+b$ не является делителем $c^p$, если $a,b,c$ являются натуральными числами.

Допустив наличие натурального решения, мы пришли к противоречию, которое доказывает: допущение было ошибочным, уравнение (7) не имеет натуральных решений.

[mihaild]

falconer в сообщении #1496611 писал(а):

левая может быть кратна $x^2y^2$ только в том случае, если $xy\;\left|\;\left[(x+y)^2-z^2\right] \text{ и } xy\; \right|\;\left[(x+y)^2+z^2\right]$

Переход не обоснован.

falconer в сообщении #1496611 писал(а):

Т.е., если $xy$ является делителем $z^2$

Переход не обоснован.

[falconer]

$$ \left[\left(x+y\right)^2-z^2-2xy\right]\left[\left(x+y\right)^2+z^2-2xy\right]=2x^2y^2$$

$$ \left[\frac{\left(x+y\right)^2-z^2}{xy}-2\right]\left[\frac{\left(x+y\right)^2+z^2}{xy}-2\right]=2$$

-- 15.12.2020, 18:49 --

Ответ на сообщение mihiv.

Откуда это следует? Пусть $z=dk$, ($k,d-$ взаимно просты), а $x+y=d^p$, Тогда $(x+y,z)=d<z$, но $z^p$ делится на $x+y$.


Давайте проанализируем ваше предположение.

Пусть $ z=dk $, $x+y=d^p$. Согласно лемме эти значения должны удовлетворять неравенству

$$ 1 < \frac{x+y}{z}=\frac{d^{p-1}}{k} < \sqrt[p]{2^{p-1}}$$

и

$$ d^{p-1}=\alpha k$$

$$ x+y=d^p=\alpha kd $$

где

$$1<\alpha<\sqrt[p]{2^{p-1}}$$

Разделив $z^p$ на $x+y$

$$ \frac{z^p}{a+b}=\frac{d^pk^p}{\alpha kd}=\frac{d^{p-1}k^{p-1}}{\alpha},$$

натурального числа не получаем!

[Valprim]

falconer в сообщении #1496611 писал(а):

Из последнего равенства видно, что в любом натуральном решении правая часть кратна $x^2y^2$, а левая может быть кратна $x^2y^2$ только в том случае, если

$$xy\;\left|\;\left[(x+y)^2-z^2\right] \text{ и } xy\; \right|\;\left[(x+y)^2+z^2\right]$$

А если так:

$$x^2\;\left|\;\left[(x+y)^2-z^2\right] \text{ и } y^2\; \right|\;\left[(x+y)^2+z^2\right]$$

то противоречий нет.

falconer в сообщении #1496620 писал(а):

Разделив $z^p$ на $x+y$

$$ \frac{z^p}{a+b}=\frac{d^pk^p}{\alpha kd}=\frac{d^{p-1}k^{p-1}}{\alpha},$$

натурального числа не получаем!

Подставляем $d^{p-1}=\alpha k$ получаем:

$$ \frac{d^{p-1}k^{p-1}}{\alpha}= \frac{\alpha k k^{p-1}}{\alpha}=k^p,$$

И снова нет противоречий.

[falconer]

1)

Вывод необходимости деления $z^$ на $xy$ следует из

$$\left[\frac{\left(x+y\right)^2-z^2}{xy}-2\right]\left[\frac{\left(x+y\right)^2+z^2}{xy}-2\right]=2$$

А в тексте, при преобразовании исходного уравнения $x^4+y^4=z^4$, я остановился на

$$\left[\left(x+y\right)^2-z^2-2xy\right]\left[\left(x+y\right)^2+z^2-2xy\right]=2x^2y^2$$

Думал и так все очевидно. Вы же прелагаете довести преобразование исходного уравнения до

$$\left[\frac{\left(x+y\right)^2-z^2}{x^2}-\frac{2y}{x}\right]\left[\frac{\left(x+y\right)^2+z^2}{y^2}-\frac{2x}{y}\right]=2$$

И где тут нет противоречия?

2) Получая $x+y=\alpha d k$, была использована подстановка $d^{p-1}=\alpha k$. Вы прелагаете использовать ее повторно, откатываясь назад. Фактически вы прелагаете использовать исходные значения ($x+y=d^p$, $z=dk$ в

$$ \frac{z^p}{x+y}=k^p$$

Давайте поступим иначе. Какими-бы не были значения ($x+y$ и $z$), в любом решении согласно лемме они должны удовлетворять неравенству

$$1 < \frac{x+y}{z}=\alpha < \sqrt[p]{2^{p-1}}$$

или

$$ x+y=\alpha z$$

Тогда

$$ \frac{z^p}{\alpha z}=\frac{z^{p-1}}{\alpha}$$

[nnosipov]

falconer в сообщении #1496734 писал(а):

Вывод необходимости деления $z^$ на $xy$ следует из

$$\left[\frac{\left(x+y\right)^2-z^2}{xy}-2\right]\left[\frac{\left(x+y\right)^2+z^2}{xy}-2\right]=2$$

Как именно следует, Вы не объяснили. Приведите доказательство сформулированного утверждения.

[falconer]

Это же очевидно.

Если сумма и разность двух натуральных чисел делится на какое-то число > 2, то это число является их общим делителем.
Из

$$\frac{a+b}{c}=d,\;\frac{a-b}{c}=e$$

следует

$$ a+b=cd,\;a-b=ce$$

и

$$ 2a=c(d+e),\;2b=c(d-e)$$

Следовательно, $c>2$ должно быть общим делителем $a$ и $b$.

В нашем случае $xy$ явно $>2$.

[nnosipov]

falconer
Как я понял, у Вас $c=xy$. А чему равны $a$ и $b$?

-- Ср дек 16, 2020 18:59:27 --

falconer в сообщении #1496740 писал(а):

Это же очевидно.

Напрасно Вы так думаете, это совсем не очевидно.

[mihaild]

falconer в сообщении #1496740 писал(а):

Если сумма и разность двух натуральных чисел делится на какое-то число > 2, то это число является их общим делителем

А где у вас тут сумма и разность натуральных чисел, и на какое число они делятся?

[falconer]

В выкладках $a,b,c,d,e$ взяты для краткости и никакого отношения к нашей задаче не имеют.

В нашем случае $a=(x+y)^2$, $b=z^2$, $c=xy$.

[Valprim]

falconer в сообщении #1496734 писал(а):

Вы же прелагаете довести преобразование исходного уравнения до

$$\left[\frac{\left(x+y\right)^2-z^2}{x^2}-\frac{2y}{x}\right]\left[\frac{\left(x+y\right)^2+z^2}{y^2}-\frac{2x}{y}\right]=2$$

И где тут нет противоречия?

А в чём оно?

falconer в сообщении #1496734 писал(а):

согласно лемме они должны удовлетворять неравенству

$$1 < \frac{x+y}{z}=\alpha < \sqrt[p]{2^{p-1}}\quad \text {или} \quad x+y=\alpha z$$

$$\alpha=\frac {x+y}{z}$$

- рациональная дробь. Какие проблемы?

[nnosipov]

falconer в сообщении #1496748 писал(а):

В нашем случае $a=(x+y)^2$, $b=z^2$, $c=xy$.

И откуда тогда следует, что, например, $a+b$ делится на $c$? Это надо обосновать.

По всей видимости, в равенстве

falconer в сообщении #1496734 писал(а):

$$\left[\frac{\left(x+y\right)^2-z^2}{xy}-2\right]\left[\frac{\left(x+y\right)^2+z^2}{xy}-2\right]=2$$

Вы полагаете содержимое скобок целыми числами, но это предположение ничем не обосновано.