Эллипс вписанный в параллелограмм

[DismasK]

Имеется параллелограмм $ABCD$, в него вписан эллипс и касается сторон $AB$, $BC$, $CD$, $DA$ в точках $E$,$F$,$G$,$H$. Известно отношение отрезков $AE$ и $EB$. Вопрос следующий: в каком соотношении точка $H$ делит сторону $AD$.
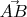
Любой четырехугольник можно свести к квадрату. Если вписать в этот квадрат эллипс, то точки касания будут симметричны, то есть делить стороны будут в одинаковом соотношении. Чтобы от квадрата перейти к параллелограмму нужно изменить образующие вектора. Если мы находимся в СК, где оси совпадают со сторонами квадрата, то один вектор $\vec{AD}$ умножить на число (растянуть), а второй $\vec{AB}$ повернуть на угол $\alpha$. При таких преобразованиях $\vec{AH}$ и $\vec{AE}$ изменяются аналогично, и отношения отрезков не меняются .
Я считал, что параллельные стороны параллелограмма эллипс делит на симметричные соотношения, например, $\frac{AE}{EB}=\frac{CG}{GD}$. Однако, строгого доказательства этому я не нашел. Верно ли мое доказательство, того, что точка $H$ будет делить сторону $AD$ в том же соотношении, что и точка $E$ делит $AB$?

[DeBill]

DismasK в сообщении #1495755 писал(а):

Верно ли мое доказательство,

Да, при условии, что будет аккуратно доказано

DismasK в сообщении #1495755 писал(а):

Если вписать в этот квадрат эллипс, то точки касания будут симметричны,

Но, вообще, лучше было "свести" эллипс к окружности (около которой описан параллелограмм, который реально будет ромбом): тогда нужное Вам утверждение последует из свойства касательных из точки к окружности (равны они).

-- 08.12.2020, 20:59 --

Ну и, конечно, надо быть чуток аккуратнее: "свести" - заменить на "аффинным преобразованием перевести в", и сослаться на свойства аффинных пр-й (отношение длин параллельных отрезков сохраняется)

[DismasK]

Благодарю за ответ!

DeBill в сообщении #1495759 писал(а):

Но, вообще, лучше было "свести" эллипс к окружности (около которой описан параллелограмм, который реально будет ромбом): тогда нужное Вам утверждение последует из свойства касательных из точки к окружности (равны они).

Да, у меня была такая мысль, но я не знал какими именно преобразованиями перевести эллипс в окружность, поэтому решил попробовать привести к квадрату все.

[ewert]

DismasK в сообщении #1495755 писал(а):

Чтобы от квадрата перейти к параллелограмму

Только наоборот -- от параллелограмма к квадрату. Потому что если от квадрата, то неизвестно, к какому эллипсу в параллелограмме мы придём.

DismasK в сообщении #1495755 писал(а):

а второй $\vec{AB}$ повернуть на угол $\alpha$

Поворот только одного вектора -- штука скользкая. Лучше сделать перекос, т.е. преобразование вида $\begin{cases}x'=x+\alpha y,\\y'=y.\end{cases}$ Оно откровенно линейно и, следовательно, не меняет относительного положения точек касания. Перекосом можно любой параллелограмм перевести в прямоугольник, а затем прямоугольник растяжением -- уже в квадрат.