Необходимо вывести уравнение прямой, которая в заданном отношении делит угол между двумя прямыми, заданными уравнениями:


Есть уравнение пучка прямых, проходящих через точку пересечения двух данных прямых:

Для биссектрисы значения

и

будут равны соответственно:

и

Пытался нагуглить, как выводятся эти коэффициенты, но нигде не нашел, всюду только готовая формула. Может кто знает, где найти доказательство?
Вот, но я бы хотел функцию для общего случая
То есть, на входе:
• уравнение 1 прямой:

• уравнение 2 прямой:

• отношение углов, на которые нужно разделить угол между данными прямыми:

На выходе:
• уравнение искомой прямой (в любом виде)
Получается, что в частном случае, когда
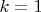
, эта функция вернет уравнение биссектрисы, т.к. полученные углы делятся в отношении один к одному
Например, при

функция вернет уравнение линии, которая делит данный угол в отношении 2 к 3
Ну или же коэффициент

на входе может означать не отношение полученных углов, а часть, которую первый полученный угол составляет от данного угла
В таком случае функция вернет уравнение биссектрисы в случае, когда

, т.к. первый полученный угол составляет половину данного угла
Соответственно уравнение линии, которая делит данный угол в отношении 2 к 3, функция вернет при

, т.к.

Не знаю, как лучше. Да и вообще без понятия, как вывести такую формулу, и возможно ли это вообще
Был бы рад получить ответ
P.S. Я не математик, так что сори если что)