Здравствуйте.
Возникла потребность посмотреть эффект Джоуля-Томсона, взял 2-й том Сивухина по общей физике

104. Эффект Джоуля-Томсона для газа Ван-дер-Ваальса, но есть пара непонятных моментов. Я немного изменю изложения в силу того, как я понял.
Рассмотрим коэффициент

, где

- энтальпия. Далее этот коэффициент преобразовывается к виду

Приравниваем

к нулю и находим отсюда температуру инверсии

как функцию

(её график - кривая инверсии). Теперь используя уравнение состояния газа

и исключая

находим инверсное давление

как функцию инверсной температуры. Далее находим обратную функцию

и строим график, который является многозначным. Итак у нас есть связь между инверсными температурой и давлением. А как мне, например, построить график функции

, которая входит в определение коэффициента

, чтобы там было видно, что в некоторой точке

функция

будет иметь точку экстремума? Нужно из уравнения состояния выразить

? Но чем заменить объем

? Мы ведь не можем использовать, например, функцию

ведь мы получали её из условия, что
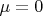
... В общем, запутался я.