Уравнение Пелля с двумя параметрами.

[TR63]

Существуют ли параметры $(y;q)\in N^+$, $(q)$-нечётное такие, что уравнение Пелля

$$z^2-(y^2+4)x^2=y^2-(200q+14)>0$$

имеет решение.

Мои попытки решения.

С помощью логических рассуждений (длинных) у меня получилось, что таких параметров не существует. Но, возможно я ошиблась и существует контрпример. Тогда его можно найти. Прошу помочь найти контрпример, если он существует.

[TR63]

TR63 в сообщении #1494646 писал(а):

Но, возможно я ошиблась и существует контрпример

Контрпример нашёлся (спасибо за помощь). Ошибку нашла. В новой формулировке задача тоже решена.

TR63 в сообщении #1494646 писал(а):

Существуют ли параметры $(y;q)\in N^+$, ... такие, что уравнение Пелля

$$z^2-(y^2+4)x^2=y^2-(200q+14)>0$$

имеет решение.

TR63 в сообщении #1495704 писал(а):

рассмотреть ... уравнение относительно существования решения в зависимости от последней цифры у параметра $(y)$.

TR63 в сообщении #1495570 писал(а):

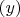
2).$z^2-(y^2+4)x^2=y^2-(200q+14)>0$

У меня получилось, что, если решение существует, то $(x;y)$ должны быть нечётными. Тогда рассмотрим, каким должно быть $(z)$, чтобы решение существовало. Получим:
1). $y=10k+1$, $(z)$ не существует
2). $y=10k+3$, возможные последние цифры $(z^2)=(0_+;2_-;8_-)$
3). $y=10k+5$, возможные последние цифры $(z^2)=(0_+;2_-;6_?)$
4). $y=10k+7$, возможные последние цифры $(z^2)=(0_+;2_-;8_-)$
5). $y=10k+9$, $(z)$ не существует

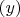
Т.е. надо выяснить, существует ли решение, если последняя цифра параметра $(y)$ равна $(...;5)$.

при $z=10m+(4;6)$, $y=10k+5$
с помощью логических рассуждений у меня получилось, что решений не существует.
При $z=10m$ существование решений нашёл Andrey A.