Это на какой же олимпиаде такую задачу дали?
Что-то никто эту задачу решать не хочет.
Я не буду детально выписывать решение, но ничего сложного там нет.
Будем рассматривать
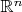
с

, рассматривая его как множество всевозможных упорядоченных

-ок

действительных чисел, снабжённое стандартной алгебраической структурой и стандартной евклидовой метрикой. Компоненты

-ки называются её координатами, началом координат называется нулевая

-ка

. Для положительного действительного числа

символом

будем обозначать открытый шар радиуса

с центром в начале координат,

— сферу радиуса

с центром в начале координат.
Кроме того, для каждого шара

и каждой точки

обозначим

какую-нибудь ретракцию множества

на множество

. (Ретракцией топологического пространства

на его подмножество

называется такое непрерывное отображение

, что

является тождественным отображением, то есть, для каждой точки

выполняется равенство

.)
Конкретный пример такой ретракции можно получить, определив её как центральную проекцию из точки

множества

на сферу

, продолженную вне шара тождественным отображением.
Мы докажем, что нарост любой компактификации пространства
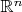
связен.
Достаточно рассмотреть только компактификацию Стоуна–Чеха, поскольку любая другая хаусдорфова компактификация является образом компактификации Стоуна–Чеха при непрерывном отображении, оставляющем точки компактифицируемого пространства неподвижными, а непрерывный образ связного множества связен. Но никакие специфические свойства компактификации Стоуна–Чеха в доказательстве не нужны, поэтому можно рассматривать сразу произвольную компактификацию.
В одномерном случае годится аналогичное рассуждение с небольшими отличиями: доказывается, что нарост полупрямой

(или
![$(-\infty,0]$ $(-\infty,0]$](https://dxdy-01.korotkov.co.uk/f/c/8/8/c889590104be3ba29df8e0f77d56213e82.png)
) связен, все точки выбираются только на соответствующей полупрямой, и не понадобится ретракция.
Для упрощения выражений удобно отождествить пространство с его образом в компактификации, то есть, в обозначениях из первого сообщения, считать, что

и

— одно и то же множество, а вложение

является тождественным.
Рассмотрим произвольную хаусдорфову компактификацию

пространства
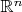
,

, и пусть

— нарост.
Так как пространство
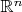
локально компактно, оно является открытым подмножеством в любой своей хаусдорфовой компактификации, а нарост, таким образом, является замкнутым и нигде не плотным.
Предположим, что нарост

не связен. Тогда существуют такие непустые замкнутые (в самом наросте, и, следовательно, во всей компактификации) подмножества
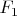
и
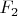
, что

и

. Наша цель — построить последовательность точек
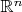
, которая содержит бесконечное множество различных точек, но не имеет предельных точек ни в
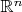
, ни в
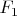
, ни в
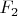
. Это будет означать, что

не компактно, а это, естественно, противоречит определению компактификации. Поэтому предположение о несвязности нароста ложно.
Так как хаусдорфово компактное пространство нормально, множества
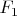
и
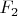
имеют такие открытые окрестности

и

, что их замыкания
![$\Phi_1=[UF_1]_{v\mathbb R^n}$ $\Phi_1=[UF_1]_{v\mathbb R^n}$](https://dxdy-04.korotkov.co.uk/f/f/2/7/f27f830b4b1619737a6e3c304defe71882.png)
и
![$\Phi_2=[UF_2]_{v\mathbb R^n}$ $\Phi_2=[UF_2]_{v\mathbb R^n}$](https://dxdy-03.korotkov.co.uk/f/6/f/3/6f31d48e2d41c39556d0c5b748017eac82.png)
не пересекаются.
Заметим, что множества

и

оба замкнуты в
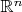
, но не замкнуты в

, так как в противном случае хотя бы одно из множеств

или

было бы открытым в

, что невозможно, так как нарост компактификации не может содержать открытое множество. Из этого следует, что эти множества не ограничены в
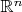
.
Вследствие нормальности

существует такая непрерывная функция
![$g\colon v\mathbb R^n\to[0,1]$ $g\colon v\mathbb R^n\to[0,1]$](https://dxdy-01.korotkov.co.uk/f/4/1/b/41b5f92ad023807a15dcedc0db2d059182.png)
, что

для всех

и

для всех

.
Теперь для каждого

множества

и

не являются пустыми. Выберем в них по точке

и

и определим непрерывную вектор-функцию
![$\mathbf h_k\colon[0,1]\to\mathbb R^n$ $\mathbf h_k\colon[0,1]\to\mathbb R^n$](https://dxdy-02.korotkov.co.uk/f/1/6/c/16c47182c58002ce6d7b0b0c4990849b82.png)
формулой

,
![$t\in[0,1]$ $t\in[0,1]$](https://dxdy-01.korotkov.co.uk/f/4/8/9/489dfef0eefc2611fce620116590ce8982.png)
. Образ отрезка
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
при этой вектор-функции представляет собой отрезок прямой в пространстве
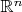
, соединяющий точки

и

. Этот отрезок может пересекать шар

, но заведомо его не покрывает, поэтому существует точка

, не принадлежащая указанному отрезку. Воспользуемся описанной выше ретракцией

и получим другую непрерывную вектор-функцию

, для которой образ отрезка
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
лежит вне шара

.
Определим непрерывную функцию
![$g_k\colon[0,1]\to[0,1]$ $g_k\colon[0,1]\to[0,1]$](https://dxdy-04.korotkov.co.uk/f/7/9/6/7966fe57fe0022c6158bb18249fe4c8182.png)
формулой

. Легко вычислить, что

,

. Так как функция, непрерывная на отрезке, принимает на нём все значения, промежуточные между значениями на концах, существует такая точка
![$t_k\in[0,1]$ $t_k\in[0,1]$](https://dxdy-02.korotkov.co.uk/f/d/e/7/de7839b70880e7d610ea8cbe035edd2a82.png)
, что

. Обозначим

. Точка

лежит вне шара

.
Последовательность точек

удовлетворяет заявленным требованиям, то есть, содержит бесконечное множество различных точек, но не имеет предельных точек ни в
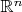
, ни в
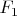
, ни в
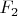
.
Уточнение деталей и вообще наведение марафета оставляю читателям, поскольку я уже утомился всё это писать.
Если уважаемый
Padawan имел в виду какое-нибудь изящное решение, прошу его изложить.