Мода

[Solaris86]

Непонятно про бимодальное распределение.

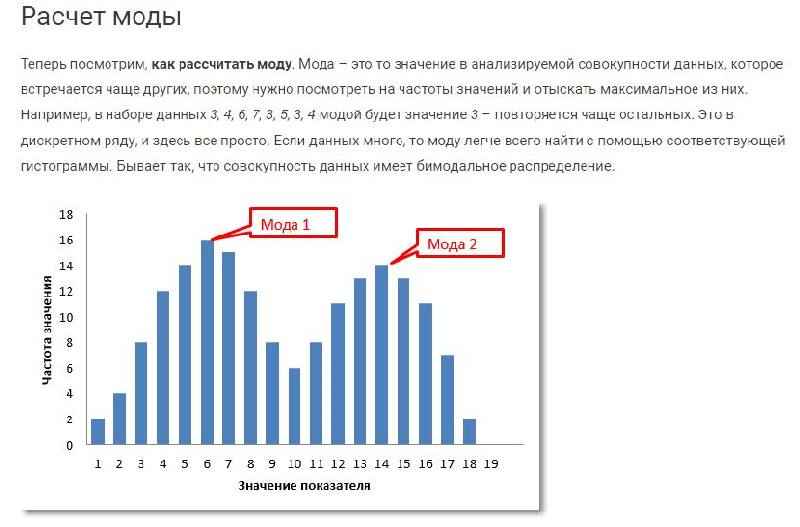
Допустим, есть ряд: 1, 2, 3, 4, 4, 5, 6, 7, 7, 7, 8, 9, 10.
По определению, мода - наиболее часто встречающееся значение в ряду, что в данном ряду означает, что мода - 7, т.к. встречается 3 раза.
А вот если ориентироваться на картинку с бимодальным распределением, то моды в этом ряду две: первая мода - 4, вторая мода - 7...
Как правильно?

[EUgeneUS]

Solaris86
Всё таки лучше идти от определения к его объяснению, чем наоборот.
Можно воспользоваться таким определением:

Цитата:

Модой абсолютно непрерывного распределения называют любую точку локального максимума плотности распределения. Для дискретных распределений модой считают любое значение $a_i$, вероятность которого $p_i$ больше, чем вероятности соседних значений

Исходя из него, в Вашем примере $7$ и $4$ являются модами.

[alisa-lebovski]

Определение моды в приведенном отрывке, конечно, противоречиво. Авторам незачет.