Наверняка не интегральный. Не исключено, что имелась в виду малоизвестная теорема Коши про

(например, Зорич, глава 3, параграф 1, пункт 4 (про ряды), утверждение 2 (после примера 28).
Критерий Коши здесь, конечно, притянут несколько за уши. Но можно и поизвращаться. Сумма начиная с любого номера

оценивается сверху через сумму от

до

, плюс сумму от

до

, плюс сумму от
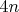
до

и т.д. (это, собственно, и есть идея доказательства той теоремы Коши). Оценивая грубо каждую подсумму через начальное слагаемое, получим сумму фиксированной геометрической прогрессии, умноженную на отрицательную степень

; вот вам и критерий Коши, если угодно.
А почему это извращение -- потому, что фактически здесь задействован не критерий Коши, а более примитивная теорема: для знакоположительных рядов сходимость равносильна ограниченности.
-- Сб ноя 21, 2020 12:03:38 --Предела точно нет. Но и ряда тоже.
А ряд и не обязателен. Наверняка имелась в виду
последовательность тех сумм.