Интегральное уравнение первого рода сверточного типа

[sup]

Рассмотрим уравнение Вольтерры первого рода сверточного типа с ядром $K(t)$

$$ \int \limits_0^t K(t - \tau)u(\tau) \, d\tau = f(t), \quad t > 0. \eqno (1) $$

Это линейное уравнение, по виду похожее на эволюционное. Однако для него, как оказывается, из локальной разрешимости не вытекает глобальная.
Предлагаю построить пример такой финитной функции $K(t)$, что для любой достаточно гладкой (конечная гладкость) финитной функции $f(t)$ решение локально существует, но не продолжается на всю полуось $(0, \infty)$.

Для ОДУ непродолжаемость решений --- свойство нелинейных уравнений. Непродолжаемость решения каких-то линейных уравнений выглядит неожиданным и весьма странным фактом. Хотя примеры, как оказалось, очень простые.

Тем, кому эта задачка покажется слишком простой (а так оно и есть), можно предложить другую. Наивный подход к решению уравнения (1) предполагает использовать преобразование Лапласа. Но, как мы только что видели, это не всегда возможно. Тем не менее, можно указать условия разрешимости уравнения (1) на конечном интервале $(0,T)$ в терминах образа $\hat K(s)$.

Докажите, что для разрешимости уравнения (1) на интервале $(0,T)$ для любой достаточно гладкой финитной на полуоси функции $f(t)$ необходимо и достаточно, чтобы в некоторой полуплоскости $\operatorname{Re} s \geqslant \sigma > 0$ для некоторых $C_1, C_2, \nu > 0$ выполнялось условие

$$ |\hat K(s)| \geqslant \frac{C_1}{|s|^{\nu}} - C_2e^{- T\operatorname{Re} s}. $$

''Подсказка''. При выполнении этого условия, для решения можно указать явную формулу.

[sup]

Задача, похоже, не вызвала особого интереса. А между тем, вопрос-то весьма любопытный. Начать с того, что единственность при минимальных естественных условиях известна очень давно (Титчмарш. Введение в теорию интегралов Фурье.). А вот с разрешимостью проблемы.
Один из типичных способов решения таких уравнений --- с помощью дифференцирования получить уравнение второго рода. Этот прием сработает, если функция $K(t)$ гладкая и найдется ненулевая производная $K^{(n)}(0) \neq 0$. А если гладкость закончится раньше, или все производные нулевые? Кстати, данный подход показывает, что гладкость решения может быть существенно хуже гладкости правой части $f(t)$. Например, для $K(t) = t^n$ имеем $u(t) = f^{(n + 1)}(t) / n!$. Кроме гладкости, правая часть еще и должна иметь нуль ''подходящего'' порядка при $t = 0$, но это сейчас не важно. Значит решения нашего уравнения способны со временем терять гладкость. Действительно, при $z > 1$ значения $u(z)$ можно определять из уравнения

$$ \int \limits_0^{t } K(t - \tau) u(1 + \tau) \, d\tau = f(1 + t) - \int \limits_0^1 K(1 + t - \tau) u(\tau) \, d\tau = f(t) - g(t). $$

Но в правой части появляется функция $g(t)$, которая может быть менее гладкая, чем $f(t)$. Из этих соображений уже легко строится искомый пример. Положим

$$ \begin{cases} &K(t) = t, \quad 0 < t < 1, \\ &K(t) = 0, \quad 1 < t. \end{cases} $$

Для гладкой $f(t)$, такой, что $f(0) = f'(0) = 0$ имеем

$$ \begin{cases} &u(t) = f''(t), \quad 0 < t < 1, \\ &u(t) = f''(t) + u(t - 1) + u'(t - 1), \quad 1 < t. \end{cases} $$

Из этой формулы видно, что гладкость решения уменьшается при переходе через $t = 1,2,3 \dots$.

А что с преобразованием Лапласа?
Если совершенно формально как-то продолжить все функции на полуось $t > 0$ и применить преобразование Лапласа, то получим

$$ \hat u(s) = \frac{\hat f(s)}{\hat K(s)}. $$

Отсюда видна главная проблема. Знаменатель может быть малым или даже нулевым. У нас есть определенный произвол в выборе продолжений функций $K(t), f(t)$, но совершенно непонятно как им ''грамотно'' распорядиться. Как убрать возможные особенности $\hat u(s)$ в некоторой полуплоскости $\operatorname{Re} s \geqslant \sigma_0$? Кроме этого, надо еще и обеспечить сходимость интеграла в обратном преобразовании

$$ u(t) = \frac{1}{2 \pi i}\int \limits_{\operatorname{Re} s = \sigma_0}e^{st}\frac{\hat f(s)}{\hat K(s)}\, ds. $$

Оказывается, все не так уж и сложно. Не надо искать какие-то замечательные продолжения функций. Надо просто сдвинуть контур интегрирования в ту область, где $\hat K(s)$ ведет себя ''хорошо''. Просто так отодвинуть прямую не получается. Нужен ''кривой'' контур. Отметим, что этому мешает экспонента $e^{st}$. Под интегралом для экспоненты мы можем позволить себе не более чем степенной рост по $|s|$. 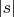Этот рост можно скомпенсировать быстрым (степенным) убыванием $\hat f(s)$. Такое убывание дает гладкость $f(t)$ и нужное обращение в 0 при $t = 0$. Таким образом, на контуре мы должны иметь что-то типа

$$ |e^{sT}| \sim |s|^m, \quad s \in \Gamma. $$

Правее этого контура требуется поведение от $\hat K(s)$. Легко видеть, что все это как раз и обеспечивается условием

$$ |\hat K(s)| \geqslant \frac{C_1}{|s|^{\nu}} - C_2e^{-T \operatorname{Re} s}. \eqno(2) $$

Таким образом мы получили формальное представление для решения при $0 < t < T$. Легко убедиться, что это действительно решение. Значит условие (2) достаточно для разрешимости уравнения (1), при условии, что правая часть достаточно гладкая и как-то-там обращается в 0 при $t = 0$. Но условие (2) и необходимо для разрешимости уравнения (1). Для этого достаточно рассмотреть $f(t) = t^n$. Пусть $n$ таково, что решение существует при $0 < t < T$

$$ \int \limits_0^{t } K(t - \tau) u(\tau) \, d\tau = t^n. $$

Все функции продолжаем нулем при $t > T$.
Умножим это уравнение на $e^{st}$ и проинтегрируем по $(0,T)$. После нехитрых преобразований легко получаем

$$ \hat K(s) \hat u(s) = \frac{n!}{s^{n+1}} + O(e^{-T \operatorname{Re} s}). $$

Отсюда следует условие (2).

К сожалению, с практической точки зрения от этих результатов мало толку. Хотя и удается строить разные экзотические примеры. Например, такой пример несуществования локального решения.


Пусть $\hat K(s)$ имеет бесконечное количество нулей на вещественной полупрямой $\operatorname{Im} s = 0$. Тогда уравнение

$$ \int \limits_0^{t } K(t - \tau) u(\tau) \, d\tau = f(t) $$

не разрешимо ни на каком интервале $(0,T)$ для любой нетривиальной функции $f(t) \geqslant 0$. Ни гладкость, ни обращение в нуль, ничего не помогает. Для доказательства достаточно рассмотреть частичное преобразование Лапласа (как и при доказательстве необходимости) с конкретными значениями $s_k$ --- вещественными нулями $\hat K(s)$, и устремить $k \to \infty$. Левая и правая часть равенства будут иметь разную скорость стремления к 0.

Еще один экзотический пример. Можно указать негладкое ядро $K(t)$, у которого даже нет конечной вариации в окрестности $t = 0$, а разрешимость уравнения есть.
Это просто ступенчатая функция со значениями 0 и 1, которая ''нужным'' образом осциллирует в окрестности $t = 0$. Для нее можно проверить справедливость условия (2).