Около года назад я опубликовал результат по числу ГП ладьи на доске

где просил о помощи с вычислением значений по формуле на PARI. Теперь мне бы хотелось описать цепочку рассуждений, благодаря которой я пришел к результату, попросить помощи в корректировании описания хода рассуждений и восполнении пробела, который возник ввиду того, что я долгое время не возвращался к этой проблеме.
Все что будет ниже до определенного момента - это последовательные рассуждения.
Начнем с элементарного случая

. 1-ую клетку выбираем

способами, 2-ую клетку выбираем

способами, перемножаем способы. Продолжая далее будем иметь
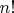
ГП ладьи на доске

.
Ладья

. Вводим заранее размещаемые элементы - змейки и лестницы, занимающие по 2 клетки или один полный столбец. Разместим 1 лестницу в любом столбце, начинаем движение с любой из нижних клеток, заканчиваем на любой из нижних (

ГП), далее проходим через лестницу и начинаем так же на любой, заканчиваем на любой (

ГП). Перемножая будем иметь

ГП.
Размещаем змейку. Аналогично начинаем вверху, проходим через змейку, заканчиваем внизу. Если поменять строки клеток местами, это будет не змейка, а лестница, т.е. эти 2 случая симметричны и достаточно исследовать, например, лестницу, что мы уже практически сделали выше, а затем удвоить результат. Лестницу мы можем разместить в любой из столбцов

способами, итого

ГП.
1 лестница и 1 змейка. Здесь мы можем разбить посещение нижних клеток на 2 этапа. На 1-ом этапе мы можем посетить от

до

клеток, которые мы выбираем из

клеток:

Затем мы их посещаем начиная с любой и заканчивая на любой, т.е.

Когда мы проходим через лестницу, мы обходим все верхние клетки до посещения змейки, т.е.

и проходя через змейку посещаем все оставшиеся нижние клетки

По итогам имеем

Змейку и лестницу мы размещаем

способами или

способами, итого

ГП.
2 лестницы и 1 змейка. Случай 2 змейки и 1 лестница симметричен, если поменяем строки местами. Т.е. достаточно аналогично рассмотреть какой-нибудь один из случаев. Здесь посещение верхних клеток также разбивается на 2 этапа.


итого

ГП.
Далее 2 змейки и 2 лестницы, тут уже 3 этапа внизу:


итого

ГП.
Далее

затем

еще далее

В общем виде угадывается формула для нечетного набора змеек и лестниц

для четных аналогично

Если ввести функцию

, такую, что

, то


В общем виде

Все это помещаем под сумму и удваиваем ввиду симметрий (1 л и 1 з; 1л, 1з; 1 з и 2 л, 2 з и 1 л; 2 л, 2 з; и т.л.):

Поиск в OEIS приводит нас к
A096121 где описание последовательности соответствует полученному результату. К последовательности мною когда-то добавлялась формула, в которой мы приходим к еще одной последовательности, что интересно рекуррентной, если выносим из выражения

.
Для наглядного иллюстрирования разбиения на этаы мы могли бы обозначать:
1 лестница -
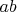
- переход с нижней строки (

) на верхнюю (

).
1 лестница -
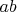

1 змейка

1 лестница 1 змейка -


1 змейка 1 лестница

и т.д. Получаются строки из элементов

типа
ab, aba, abab, ababa
ba, bab, baba, babab
нижние тождественны из-за симметрии верхним.
Ладья

. Тут уже более расширенная симметрия

Исходной строкой будет ab. Мы будем генерировать также недопустимые здесь случаи ab, aba, abab и т.д. для удобства. Все случаи для

мы будем учитывать через:
aba
abc
abab
abac
abca
abcb
ababa
ababc
abaca
abacb
abcab
abcac
abcba
acbcb
Все строки симметричны относительно ab, т.е.

где за каждой парой элементов следуют некоторые другие. Кроме побочных, необходимых для корректной генерации все строки содержат как минимум по 1 элементу каждого типа (из a,b,c).
abac 321
abca 222
abcb 132
Цифры обозначают число занимаемых клеток на той или иной строке клеток. Промежуточные клетки не занимаются лестницами и змейками (пока что, эти случаи мы учтем далее), т.е. это можно отразить как перепрыгивание через 1 клетку.
Все вышеуказанные случаи реализуемы через



По опыту

при разбиении на 2 этапа у нас

, при разбиении на 3 этапа у нас

, соответственно без разбиения на этапы

. Индекс

в

отражает число разбиений, которые в случае

вырастают из строкиз элементов a,b,c.
Откуда нам взять тройки чисел (3,2,1), (2,2,2), (1,3,2)? Мы можем задавать строки из элементов a,b,c функцией. Еще удобнее ввести функцию для последнего элемента строки, т.к. каждая новая строка генерирует две последующих и т.д.
Если обозначить a - 0, b - 1, c - 2, то нам нужна функция, которая превращает
Такая функция существует, это
![$h(n,k)=[n=1]\cdot[k=0]+[n>1]\cdot[0\leqslant k<2^{n-1}]\cdot\left(1+k \operatorname{mod} 2 + \left\lfloor\frac{k \operatorname{mod} 2 - h(n-1,\left\lfloor\frac{k}{2}\right\rfloor)}{2}\right\rfloor\right)$ $h(n,k)=[n=1]\cdot[k=0]+[n>1]\cdot[0\leqslant k<2^{n-1}]\cdot\left(1+k \operatorname{mod} 2 + \left\lfloor\frac{k \operatorname{mod} 2 - h(n-1,\left\lfloor\frac{k}{2}\right\rfloor)}{2}\right\rfloor\right)$](https://dxdy-01.korotkov.co.uk/f/4/1/7/417a35690b353c93c7c7265786a28c4282.png)
Строки тогда представляются как цепочки элементов на дереве
0
|
1
| \
0 2
| \ | \
1 2 0 1
|\ |\ |\ |\
0 2 0 1 1 2 0 2
|\ |\ |\ |\ |\ |\ |\ |\
1201120202011201
каждый новый срез свзяан с предыдущим, а именно:
1) за исключением 1-го элемента 1-ая половина каждого нового среза полностью повторяет предыдущий;
2) вторая половина - либо зеркальное отражение первой с заменой 0 -> 2, 1 без изменений, 2 -> 0, либо копия первой половины за исключением крайних значений, что отражено мною сегодня в
https://oeis.org/draft/A091297 (схожая последовательность где 0 -> 2, 2 -> 0).
Последние 2 факта позволяют нам задавать

через одномерный массив, а именно

.
Вычислять число занятых клеток на той или иной строке из которых вытекает число разбиений на этапы мы будем специальной функцией
![$f(i,n,k)=[0\leqslant i<2]\cdot[n=1]\cdot[k=0]+[0\leqslant i<3]\cdot[n>1]\cdot[0\leqslant k<2^{n-1}]\cdot\left(f(i,n-1,\left\lfloor\frac{k}{2}\right\rfloor)+[i=h(n,k)]\right)$ $f(i,n,k)=[0\leqslant i<2]\cdot[n=1]\cdot[k=0]+[0\leqslant i<3]\cdot[n>1]\cdot[0\leqslant k<2^{n-1}]\cdot\left(f(i,n-1,\left\lfloor\frac{k}{2}\right\rfloor)+[i=h(n,k)]\right)$](https://dxdy-01.korotkov.co.uk/f/c/9/a/c9aa4aed1c98821d0d09961b2171a7e282.png)
Отсюда мы получаем заготовку

где
![$A=n-2f(i,j,k)+[i=0]+[i=h(j,k)]$ $A=n-2f(i,j,k)+[i=0]+[i=h(j,k)]$](https://dxdy-02.korotkov.co.uk/f/5/c/8/5c8877eba42bc652b1d3d7695bc9cb9a82.png)
От числа
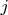
зависит число размещаемых змеек и лестниц. По промежуточным итогам имеем:

где \binom{n}{j}j! служит для учета вариантов размещения змеек и лестниц постолбцово. Необходимо также учесть вставку промежуточных элементов, о которой упоминалась ранее и которую мы реализуем через (дополнительно домножая на
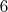
ввиду симметрии и добавляя постолбцовые пробеги)

где мы присваиваем
![$A=n-2f(i,j,k)+[i=0]+[i=h(j,k)]-\sum\limits_{q=0}^{j-1}[i=g(j-q,\left\lfloor\frac{k}{2^q}\right\rfloor)]\cdot L(p,q)$ $A=n-2f(i,j,k)+[i=0]+[i=h(j,k)]-\sum\limits_{q=0}^{j-1}[i=g(j-q,\left\lfloor\frac{k}{2^q}\right\rfloor)]\cdot L(p,q)$](https://dxdy-03.korotkov.co.uk/f/2/5/7/25778248669f791ad2645f26836ee2b982.png)

![$g(n,k)=[n=1]\cdot[k=0]\cdot2+[n>1]\cdot[0\leqslant k<2^{n-1}]\cdot h(n,k+(-1)^k)$ $g(n,k)=[n=1]\cdot[k=0]\cdot2+[n>1]\cdot[0\leqslant k<2^{n-1}]\cdot h(n,k+(-1)^k)$](https://dxdy-03.korotkov.co.uk/f/2/1/6/216b82bd3ba0081db93fd52b8383a0ba82.png)

- функция для вставляемого промежуточного элемента, который отличен от соседствующих, напр ab -> A(C)B ввиду особенности строк из элементов a,b,c (2 элемента одного типа не могут располагаться рядом, существует единственный вариант промежуточного элемента, который должен быть отличен от пары соседствующих).
На этом мои рассуждения подходят к концу. Пробел выражается в выводе формулы для реализации учета промежуточных элементов - за год я совершенно забыл как именно я это реализовывал и почему все в итоге выглядит именно так. Буду признателен за любые комментарии. Кроме того, буду рад, если эти рассуждения послужат основой для, например, чьей-либо статьи (меня там указывать вообще необязательно). Сам результат размещен вот тут -
A329319.