Пусть для целых

справедливо

.
Тогда
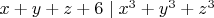
.
Помогите доказать или найти контрпример.
(мои попытки)
Преобразовал исходное уравнение в форму Пелля

и численно проверил на большом диапазоне значений

как параметра - утверждение выполняется.
При помощи оператора Результант можно показать, что

, но это вроде бы не доказывает утверждение.