Начнём с того, что атомная система единиц -- это система Хартри. То, что Вы слышали когда-то об уравнениях (методе) Хартри-Фока, не распространяет автоматически фамилию Владимира Александровича на всё, что сделал Дуглас Хартри. У В.А. хватает своих более крутых достижений, его не нужно куда-то ещё примазывать.
А это не советская традиция - приклеивать фамилии русских ученых к иностранным?

Например закон Менделеева-Клапейрона, или закон Остроградского-Гаусса
Ага. В первую очередь: а где система атомных единиц то?
Я вывел единицу длины, остальные выводятся просто
длина

(боровский радиус за единицу, и да, он обозначается не как

, а как

),
Зачем? Это выводится, я ж вывел
и то, о чём даже в Педивикии забывают
, константа Кулона
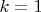
, что даёт право записывать закон Кулона как

.
Кстати да, у меня как на ру вики она не единичная. Может поэтому выражения для боровского радиуса в русской и англоязычной вики разнятся?
Нужно именно пять штук эталонов различных величин, чтоб мы могли записать уравнение Шрёдингера для произвольной системы.
Да не произвольной, а только в атоме водорода - при другом потенциале все изменится
Вывод атомной системы единиц -- задачка, ну где-то, для 8-10х классов, на ЕГЭ, в принципе, дать можно было бы.
Ни одни школьник бы с этим не справился, так что не надо судить со своей колокольни

Он просто не знал бы, что делать (и что происходит). Я знаю метод вывода в лоб - когда мы вместо метров, секунд СИ подставляем наши атомные единицы, и константы должны оединичиться. Но это скучно - а как вам мой метод, вы его точно поняли? Он для вас корректен?

Могу дать свои задачки на составление абстрактной системы единиц, где упрощается абстрактное модельное уравнение, посмотрим как вы выведите

И Вы (как я понимаю по контексту Ваших сообщений, здоровый лоб, возможно с высшим образованием) её частично решили.
Ну что сказать в столь знаменательный час, как передать всю торжественность момента?
Вы -- молодец, я лично за Вас очень счастлив. Не будь между нами экрана монитора и пандемии, я бы Вас может даже обнял, но в ввиду этих временных сложностей, я предлагаю Вам просто взять с полки пирожок.

А это уже переход на личности
