Задана бесконечная последовательность функций

определенных на числовой прямой. Докажите, что существует конечный набор функций
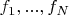
композициями которых можно записать любую функцию

.
Была идия выбрать несколько простых функций, например, линейную и экспоненту (комплексную?). И доказать, что из них можно бесконечными композициями построить ряд Тейлора для любой дифференциируемой функции... Правда

может быть недифференциируема.
Еще идея. Допустим, все функции

принимают целые значения от 0 до 9. Тогда запишем
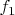
десятичной дробью

- где на i-м месте после запятой стоит значение функции

.


Тогда любую функцию

можно получить композицией функций

.
Например,

Но как теперь это обобщить? Если бы значения

были рациональными и функции

ограниченными можно было бы модифицировать данный подход.