Стереометрический тупик.

[syaomyao]

Добрый вечер! Помогите, пожалуйста, понять задачу, зашел в тупик.
В прaвильнoй трeугoльной призмe $ABCA_1B_1C_1$ сторoна oснoвания равна $4$, а бокoвое ребрo равно $2$. Точка M — середина ребра $A_1C_1$, а точка $O$ — точка пересечения диагоналей боковой грани $ABB_1A_1$.
а) Докажите, что точка пересечения диагоналей четырёхугольника, являющегося сечением призмы $ABCA_1B_1C_1$ плоскостью $AMB$ лежит на отрезке $OC_1$.
б) Найдите угол между прямой $OC_1$, и плоскостью $AMB$.

Пусть $Z$ середина $A_1B_1$ и $K$ середина $AB$, тогда построим зеленый четырехугольник $ZKCC_1$. $T$ - точка пересечения отрезков $ML$ и $ZC_1$, также она делит эти отрезки в точке пересечения пополам. Очевидно, что отрезок $KT$ лежит в плоскости $AMLB$ и плоскости $ZC_1CK$ . Назовем точку пересечения отрезков $KT$ и $C$ буковой $Q$, a точку пересечения диагоналей трапеции $AMLB$ буквой $P$. Тогда нам нужно доказать в первом пункте задачи, что точки $P$ и $Q$ совпадают.




По теореме Пифагора, получаем, что $KT=\sqrt{7}$

Из подобия треугольников $MLP$ и $APB$, мы получаем, что $TP:PK=1:2$.

Тогда, очевидно, что $TP=\dfrac{\sqrt{7}}{3}$. Теперь осталось показать, что $TQ=TP$. Но как? Я не могу понять - как разобраться в каком отношении делит точка $Q$ отрезок $KT$. Помогите, пожалуйста, разобраться?

[StaticZero]

syaomyao в сообщении #1472117 писал(а):

точку пересечения отрезков $KT$ и $C$

Каких-каких? ($ZC$, наверное).

syaomyao в сообщении #1472117 писал(а):

Но как? Я не могу понять - как разобраться в каком отношении делит точка $Q$ отрезок $KT$.

Теоремы Чевы/Менелая можно гуглить, но можно поступить умнее. Подумайте вот о чём: $ZC$ (это в прямоугольнике одна диагональ) делит $KC_1$ (другую диагональ) пополам, это очевидно. Проведите теперь $OT$.
1) $OT$ параллелен $KC_1$?
2) В каком отношении $ZC$ делит $OT$?
3) В четырёхугольнике $KOTC_1$ проведите линию, соединяющую середины $OT$ и $KC_1$. $Q$ на ней или нет?
4) Осознайте, что если ответ на 3) утвердителен, то вы выиграли.

[syaomyao]

StaticZero в сообщении #1472132 писал(а):

1) $OT$ параллелен $KC_1$?

Да? Как средняя линия!

StaticZero в сообщении #1472132 писал(а):

2) В каком отношении $ZC$ делит $OT$?

$1:1$ Так как $KC_1$ делит в таком же отношении, а далее через подобие доказывается.

StaticZero в сообщении #1472132 писал(а):

3) В четырёхугольнике $KOTC_1$ проведите линию, соединяющую середины $OT$ и $KC_1$. $Q$ на ней или нет?

Да, это трапеция. Я доказал так: в трапеции проведем прямую через середину основания и точку пересечения диагоналей, докажем, что она пройдет через середину второго основания. Доказывается это через подобие маленьких треугольников внутри трапеции. Можно было так?

[StaticZero]

syaomyao в сообщении #1472185 писал(а):

Да, это трапеция. Можно было так?

Да, всё так, только я забыл, почему я задал вопросы, которые я задал

На самом деле, как я сейчас понимаю, я хотел, чтобы вы показали, что $Q$, определённая как пересечение $ZC$ и $KT$, является как раз точкой пересечения диагоналей (меня сбивает по утру ваш рисунок, где $Q$ помечена, как будто она и есть такая точка, хотя определение вы ей дали как пересечение двух других линий). Вы доказали, и рисунок теперь у вас правильный, соответствует действительному доказательству.

Всё, теперь вам нужно выбросить $ZC$ на помойку, просто забыть про эту линию, потому что вы можете эквивалентным образом определить $Q$, как точку пересечения диагоналей в трапеции $KOTC_1$.

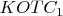
У вас там есть пара подобных треугольников в трапеции $OTQ \sim KQC_1$. $KT$ диагональ трапеции, с одной стороны, но с другой -- она хорошая линия, потому что она ещё связана позициями точек в четырёхгольнике -> вы легко найдёте её длину. Через подобие вы найдёте $QT$ (ну или $KQ$, что удобнее) и сравнением длин всё докажете.

Вам лишь нужно знать, что $P$ и $Q$ обе сразу на $KT$ лежат для того, чтобы этот трюк с длинами провернуть, но это вроде у вас доказано как раз.

[syaomyao]

Спасибо! Все понял)